


Next: Colorings of regions
Up: Definitions
Previous: Quandles
Let 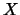 be a fixed quandle.
Let
be a fixed quandle.
Let 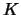 be a given oriented classical knot or link diagram,
and let
be a given oriented classical knot or link diagram,
and let 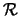 be the set of (over-)arcs.
The normals (normal vectors) are given in such a way that
the ordered pair
(tangent, normal) agrees with
the orientation of the plane (the ordered pair of the standard
be the set of (over-)arcs.
The normals (normal vectors) are given in such a way that
the ordered pair
(tangent, normal) agrees with
the orientation of the plane (the ordered pair of the standard 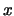 - and
- and 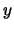 -axes),
see Fig.
-axes),
see Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
.
Figure:
Quandle relation at a crossing
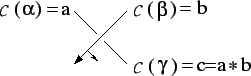 |
A (quandle) coloring 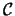 is a map
is a map
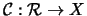 such that at every crossing,
the relation depicted in Fig.
such that at every crossing,
the relation depicted in Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) holds.
If the normal to the over-arc
holds.
If the normal to the over-arc 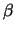 points from the
arc
points from the
arc 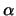 to
to 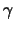 , then it is required that
, then it is required that
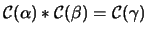 .
The pair
.
The pair 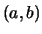 is called the ordered pair of colors at the crossing.
Let
is called the ordered pair of colors at the crossing.
Let
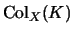 denote the set of colorings of a knot diagram
denote the set of colorings of a knot diagram 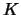 by a quandle
by a quandle 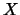 .
It is known [FeRou92] that there is a unique coloring after any Reidemeister move
given a coloring before the move, and therefore,
the cardinality
.
It is known [FeRou92] that there is a unique coloring after any Reidemeister move
given a coloring before the move, and therefore,
the cardinality
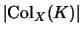 is a knot invariant.
is a knot invariant.
Note that any knot diagram is colored by a single element of a given quandle.
Such a monochromatic coloring is called trivial.
Hence for any knot 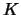 and any quandle
and any quandle 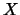 ,
,
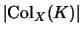 is at least
the number of quandle,
is at least
the number of quandle, 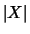 .
.
When we use Alexander quandles to color diagrams,
Inoue's Theorem [Ino01] is helpful.
There is a knot invariant called Alexander polynomial,
and an implication of Inoue's Theorem is that
a knot is colored only trivially by an Alexander quandle
![$ \mathbb{Z}_p[t, t^{-1}]/g(t)$](img62.png) if its Alexander polynomial is coprime mod
if its Alexander polynomial is coprime mod 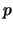 to
to 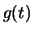 .
.



Next: Colorings of regions
Up: Definitions
Previous: Quandles
Masahico Saito - Quandle Website
2005-09-29
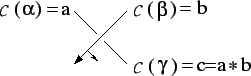
![]() and any quandle
and any quandle ![]() ,
,
![]() is at least
the number of quandle,
is at least
the number of quandle, ![]() .
.
![]() if its Alexander polynomial is coprime mod
if its Alexander polynomial is coprime mod ![]() to
to ![]() .
.