Bibliography

Ad94

C. C. Adams, The knot book, An elementary introduction to the mathematical theory of knots., W. H. Freeman and Company, New York (1994).

AG02

N. Andruskiewitsch and M. Graña, From racks to pointed Hopf algebras, Adv. in Math. 178 (2003) 177-243.

AS03*

M. Asami, S. Satoh, An infinite family of non-invertible surfaces in 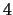$4$-space, to appear in: Bull. London Math. Soc..

Br88

E. Brieskorn, Automorphic sets and singularities, in ``Braids (Santa Cruz, CA, 1986),'' Contemp. Math. 78, Amer. Math. Soc. (1988) 45-115.

Brown82

K. S. Brown, Cohomology of Groups, Graduate Texts in Mathematics 87, Springer-Verlag (1982).

CEGS05

J.S. Carter; M. Elhamdadi; M. Graña; M. Saito, Cocycle knot invariants from quandle modules and generalized quandle cohomology, to appear in Osaka J. Math..

CENS01

J. S. Carter, M. Elhamdadi, M. A. Nikiforou, and M. Saito, Extensions of quandles and cocycle knot invariants, J. Knot Theory Ramifications 12 (2001) 725-738.

CES02

J. S. Carter, M. Elhamdadi and M. Saito, Twisted Quandle homology theory and cocycle knot invariants, Algebraic and Geometric Topology 2 (2002) 95-135.

CESS05*

J.S. Carter; M. Elhamdadi; M. Saito; S. Satoh, A lower bound for the number of Reidemeister moves of type III, Preprint, arXive.math.GT/0501490.

CHNS02

J. S. Carter, A. Harris, M. A. Nikiforou and M. Saito, Cocycle knot invariants, quandle extensions, and Alexander matrices, Suurikaisekikenkyusho Koukyuroku, (Seminar note at RIMS, Kyoto) 1272 (2002) 12-35, available at http://xxx.lanl.gov/math/abs/GT0204113.

CJKLS03

J. S. Carter, D. Jelsovsky, S. Kamada, L. Langford and M. Saito, Quandle cohomology and state-sum invariants of knotted curves and surfaces, Trans. Amer. Math. Soc. 355 (2003) 3947-3989.

CJKS01a

J. S. Carter, D. Jelsovsky, S. Kamada and M. Saito, Computations of quandle cocycle invariants of knotted curves and surfaces, Adv. in Math. 157 (2001) 36-94.

CJKS01b

J. S. Carter, D. Jelsovsky, S. Kamada and M. Saito, Quandle homology groups, their Betti numbers, and virtual knots, J. Pure Appl. Algebra 157 (2001) 135-155.

CJKS01c

J. S. Carter, D. Jelsovsky, S. Kamada and M. Saito, Shifting homomorphisms in quandle cohomology and skeins of cocycle knot invariants, J. Knot Theory Ramifications 10 (2001) 579-596.

CKS00

J. S. Carter, S. Kamada and M. Saito, Surfaces in 4-space, Encyclopedia of Mathematical Sciences142, Springer Verlag (2000).

CKS01

J. S. Carter, S. Kamada and M. Saito, Geometric interpretations of quandle homology, J. Knot Theory Ramifications 10 (2001) 345-386.

CKS03

J. S. Carter, S. Kamada and M. Saito, Diagrammatic computations for quandles and cocycle knot invariants, Contemp. Math.318(2003) Amer. Math. Soc. 51-74.

CarSai98a

J. S. Carter and M. Saito, Knotted surfaces and their diagrams, Surveys and monographs 55, Amer. Math. Soc. (1998).

CarSai03

J. S. Carter and M. Saito, Quandle Homology Theory and Cocycle Knot Invariants, in ``Proceedings of Georgia Topology Conference (2001)'' Proceedings of Symposia in Pure Math. 71 (2003) 249-269.

CSS03*

J. S. Carter; M. Saito; S. Satoh, Ribbon concordance of surface-knots via quandle cocycle invariants, J. Australian Math. Soc., to appear, available at http://xxx.lanl.gov/abs/math.GT/0309150 .

Deh00

ÊP. Dehornoy, Braids and self-distributivity, Progress in Mathematics, 192. Birkhuser Verlag, Basel (2000).

Eis02

M. Eisermann, Homological characterization of the unknot, J. Pure Appl. Algebra 177 (2003) 131-157.

EG03

P. Etingof and M. Graña, On rack cohomology, J. Pure Appl. Algebra 177 (2003) 49-59.

FeRou92

R. Fenn and C. Rourke, Racks and links in codimension two, J. Knot Theory Ramifications 1 (1992) 343-406.

FRS95

R. Fenn, C. Rourke, and B. Sanderson, Trunks and classifying spaces, Appl. Categ. Structures 3 (1995) 321-356.

FRS*

R. Fenn; C. Rourke; B. Sanderson, James bundles and applications, Preprint, available at: http://www.maths.warwick.ac.uk/${}^{\sim}$bjs/.

Fl95

J. Flower, Cyclic Bordism and Rack Spaces, Ph.D. Dissertation, Warwick (1995).

Fox61a

R. H. Fox, A quick trip through knot theory, in ``Topology of 3-manifolds and related topics (Georgia, 1961),'' Prentice-Hall (1962) 120-167.

GK03

S. Ghoneim; T. Kepka, Left selfdistributive rings generated by idempotents, Acta math. Hungar. 102 (1-2) (2003) 21-31.

Gor81

C. McA. Gordon, Ribbon concordance of knots in the 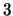$3$-sphere, Math. Ann. 257 (1981) 157-170.

Gra02a

M. Graña, Quandle knot invariants are quantum knot invariants, J. Knot Theory Ramifications 11 (2002) 673-681.

Gra02b*

M. Graña, Indecomposable racks of order 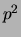$p^2$, Preprint, http://xxx.lanl.gov/abs/math.QA/0203157.

GraPre02*

M. Graña and A. Preygel, Computation of quandle cocycle invariants of knots using certain simple quandles, Talk given at the 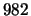$982$nd AMS meeting in Orlando, FL, Nov. 9-10, 2002.

Gre97

M. T. Greene, Some Results in Geometric Topology and Geometry, Ph.D. Dissertation, Warwick (1997).

Har03

A. Harris, Quandle Colorings of Classical Knots and Knotted Surfaces, Master's Thesis, University of South Alabama (2003).

Hata04

E. Hatakenaka, An estimate of the triple point numbers of surface-knots by quandle cocycle invariants, Topology Appl. 139 (2004) 129-144.

Ino01

A. Inoue, Quandle homomorphisms of knot quandles to Alexander quandles, J. Knot Theory Ramifications 10 (2001) 813-821.

Iwa04

M. Iwakiri, Calculation of dihedral quandle cocycle invariants of twist spun 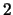$2$-bridge knots in ``Proceedings of the first East Asian School of Knots, Links, and Related Topics (Feb. 16-20, 2004)'', 85-94, available at: http://knot.kaist.ac.kr/2004/proceedings.php.

Joy82

D. Joyce, A classifying invariant of knots, the knot quandle, J. Pure Appl. Alg. 23 (1982) 37-65.

Kauff91

L. H. Kauffman, Knots and Physics, Series on Knots and Everything 1, World Sci. Publishing (1991).

Kawa90a

A. Kawauchi, The first Alexander modules of surfaces in 4-sphere, in ``Algebra and Topology'' (Taejon, 1990), Proc. KAIST Math. Workshop 5, KAIST, Taejon, Korea (1990) 81-89.

Lith85

R. A. Litherland, Symmetries of twist-spun knots, in ``Knot theory and manifolds (Vancouver, B.C., 1983),'' Lecture Notes in Math. 1144, Springer-Verlag (1985) 97-107.

Lith02*

R. A. Litherland, Quadratic quandles and their link invariants, Preprint, http://xxx.lanl.gov/abs/math.GT/0207099.

LN03

R. A. Litherland and S. Nelson, The Betti numbers of some finite racks, J. Pure Appl. Algebra 178 (2003) 187-202.

Liv93

C. Livingston, Knot theory, Carus Mathematical Monographs 24 Mathematical Association of America, Washington, DC (1993).

Lop03

P. Lopes, Quandles at finite temperatures I, J. Knot Theory Ramifications,12(2003)159-186.

Mat82

S. Matveev, Distributive groupoids in knot theory, (in Russian), Math. USSR-Sbornik 47 (1982) 73-83.

Mochi03

T. Mochizuki, Some calculations of cohomology groups of finite Alexander quandles, J. Pure Appl. Algebra 179 (2003) 287-330.

Mochi05

T. Mochizuki, The 3-cocycles of the Alexander quandles $F\sb q[T]/(T-\omega)$, Algebr. Geom. Topol. 5 (2005) 183-205.

Mura96

ÊK. Murasugi, Knot theory and its applications, Translated from the 1993 Japanese original by Bohdan Kurpita. Birkhuser Boston, Inc., Boston, MA (1996).

Nel03

S. Nelson, Classification of Finite Alexander Quandles, Proceedings of the Spring Topology and Dynamical Systems Conference. Topology Proc. 27 (2003) 245-258.

PSW04*

J. Przytycki; D. Silver; S. Williams, 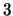$3$-manifolds, tangles, and persistent invariants, Preprint, available at: http://xxx.lanl.gov/abs/math.GT0405465.

Rose98

D. Roseman, Reidemeister-type moves for surfaces in four-dimensional space, in ``Knot theory (Warsaw, 1995),'' Banach Center Publ., Polish Acad. Sci., Warsaw, 42 (1998) 347-380.

RouSand00*

C. Rourke and B. Sanderson, A new classification of links and some calculations using it, Preprint, http://xxx.lanl.gov/abs/math.GT/0006062.

Rub83

D. Ruberman, Doubly slice knots and the Casson-Gordon invariants, Trans. Amer. Math. Soc. 279 (1983) 569-588.

Sat02

S. Satoh, Surface diagrams of twist-spun 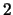$2$-knots, in ``Knots 2000 Korea, Vol. 1 (Yongpyong)'' J. Knot Theory Ramifications 11 (2002) 413-430.

Sat04*

S. Satoh, On chirality of Suzuki's 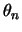$\theta_n$-curves, Preprint.

SaiSat03*

M. Saito; S. Satoh, The spun trefoil needs four broken sheets, J. Knot Theory Remifications to appear.

SatShi01b*

S. Satoh and A. Shima, Triple point numbers of surface-knots and colorings by quandles, Preprint (2001).

SatShi04

S. Satoh and A. Shima, The 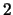$2$-twist-spun trefoil has the triple point number four, Trans. Amer. Mat. Soc. 356 (2004) 1007-1024.

Tana*

K. Tanaka, On surface-links represented by diagrams with two or three triple points, Preprint.

Taka42

M. Takasaki, Abstraction of symmetric transformations, (in Japanese), Tohoku Math. J. 49 (1942/43) 145-207.

Win84

S. Winker, Quandles, knots invariants and the 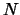$N$-fold branched cover, Ph.D. Thesis, University of Illinois at Chicago (1984).

Ze65

E. C. Zeeman, Twisting spun knots, Trans. Amer. Math. Soc. 115 (1965) 471-495.