


Next: Colorings of knot diagrams
Up: Definitions
Previous: Definitions
A quandle, 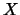 , is a set with a binary operation
, is a set with a binary operation
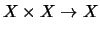 denoted by
denoted by
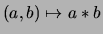 such that
(I) For any
such that
(I) For any 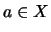 ,
,
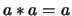 .
(II) For any
.
(II) For any 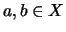 , there is a unique
, there is a unique 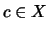 such that
such that
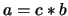 .
(III)
For any
.
(III)
For any
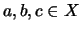 , we have
, we have
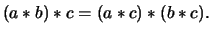 A rack is a set with a binary operation that satisfies
(II) and (III).
Racks and quandles have been studied in, for example,
[Br88,FeRou92,Joy82,Mat82].
The following are typical examples of quandles.
A group
A rack is a set with a binary operation that satisfies
(II) and (III).
Racks and quandles have been studied in, for example,
[Br88,FeRou92,Joy82,Mat82].
The following are typical examples of quandles.
A group 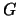 with
conjugation
as the quandle operation:
with
conjugation
as the quandle operation:
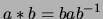 , denoted by
, denoted by 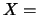 Conj
Conj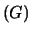 ,
is a quandle.
Any subset of
,
is a quandle.
Any subset of 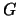 that is closed under such conjugation
is also a quandle.
Another example is the set of polynomials
that is closed under such conjugation
is also a quandle.
Another example is the set of polynomials
![$ M={\mathbb{Z}_p }[t] / f(t)$](img15.png) with mod
with mod 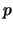 integers, for a prime
integers, for a prime 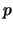 , and modulo a polynomial
, and modulo a polynomial 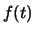 .
Then the elements of
.
Then the elements of 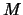 are represented by remainders of
polynomials mod
are represented by remainders of
polynomials mod 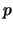 when divided by
when divided by 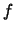 , so that
, so that 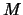 consists of
consists of
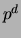 elements. A quandle structure is defined by
elements. A quandle structure is defined by
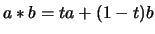 ,
, 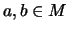 , and
it is called an Alexander quandle.
(In general, any
, and
it is called an Alexander quandle.
(In general, any
![$ \Lambda (={\mathbb{Z}}[t, t^{-1}])$](img23.png) -module
-module 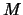 is a quandle with
is a quandle with
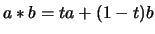 ,
, 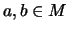 ,
that is
called an Alexander quandle.)
Classification of Alexander quandles are discussed in [Nel03].
Let
,
that is
called an Alexander quandle.)
Classification of Alexander quandles are discussed in [Nel03].
Let 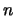 be a positive integer, and
for elements
be a positive integer, and
for elements
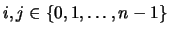 , define
, define
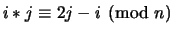 .
Then
.
Then 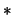 defines a quandle
structure called the dihedral quandle,
defines a quandle
structure called the dihedral quandle,
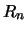 .
This is an Alexander quandle
.
This is an Alexander quandle
![$ R_n=\mathbb{Z}_n[t]/(t+1)$](img29.png) .
.
A map
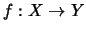 between quandles
between quandles 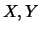 is
a quandle homomorphism if
is
a quandle homomorphism if
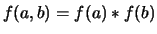 for any
for any
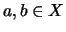 ,
where we abuse notation and use
,
where we abuse notation and use 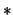 for quandle operations on different quandles
unless confusion arises.
A quandle homomorphism is an isomorphism if it is surjective and injective.
If there is an isomorphism between two quandles, they are called
isomorphic.
for quandle operations on different quandles
unless confusion arises.
A quandle homomorphism is an isomorphism if it is surjective and injective.
If there is an isomorphism between two quandles, they are called
isomorphic.
If 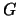 is a group and
is a group and 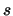 is an automorphism,
is an automorphism,
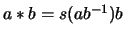 defines a quandle structure on
defines a quandle structure on 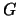 ,
and if
,
and if 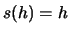 for for all
for for all 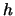 in a subgroup
in a subgroup 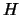 , then
, then 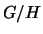 inherits the operation:
inherits the operation:
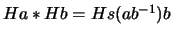 . This example is due to Joyce [Joy82], where it is proved
that
any homogeneous quandle,
. This example is due to Joyce [Joy82], where it is proved
that
any homogeneous quandle, 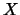 , is isomorphic to such a quandle:
Let
, is isomorphic to such a quandle:
Let
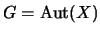 , let an element
, let an element 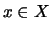 be fixed, let
be fixed, let
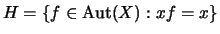 . For any element
. For any element 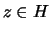 ,
,
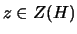 (centralizer). Then the evaluation map
(centralizer). Then the evaluation map 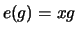 provides the isomorphism.
provides the isomorphism.



Next: Colorings of knot diagrams
Up: Definitions
Previous: Definitions
Masahico Saito - Quandle Website
2005-09-29
![]() between quandles
between quandles ![]() is
a quandle homomorphism if
is
a quandle homomorphism if
![]() for any
for any
![]() ,
where we abuse notation and use
,
where we abuse notation and use ![]() for quandle operations on different quandles
unless confusion arises.
A quandle homomorphism is an isomorphism if it is surjective and injective.
If there is an isomorphism between two quandles, they are called
isomorphic.
for quandle operations on different quandles
unless confusion arises.
A quandle homomorphism is an isomorphism if it is surjective and injective.
If there is an isomorphism between two quandles, they are called
isomorphic.
![]() is a group and
is a group and ![]() is an automorphism,
is an automorphism,
![]() defines a quandle structure on
defines a quandle structure on ![]() ,
and if
,
and if ![]() for for all
for for all ![]() in a subgroup
in a subgroup ![]() , then
, then ![]() inherits the operation:
inherits the operation:
![]() . This example is due to Joyce [Joy82], where it is proved
that
any homogeneous quandle,
. This example is due to Joyce [Joy82], where it is proved
that
any homogeneous quandle, ![]() , is isomorphic to such a quandle:
Let
, is isomorphic to such a quandle:
Let
![]() , let an element
, let an element ![]() be fixed, let
be fixed, let
![]() . For any element
. For any element ![]() ,
,
![]() (centralizer). Then the evaluation map
(centralizer). Then the evaluation map ![]() provides the isomorphism.
provides the isomorphism.