


Next: -Cocycle invariants
Up: Definitions
Previous: Colorings of knot diagrams
For a coloring
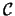 of a knot diagram
of a knot diagram 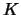 ,
there is a coloring of regions
that extend
,
there is a coloring of regions
that extend
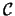 as depicted in Fig.
as depicted in Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
A coloring of regions is an assignment of quandle elements to regions
that satisfies the following requirement: Suppose the two regions
.
A coloring of regions is an assignment of quandle elements to regions
that satisfies the following requirement: Suppose the two regions 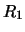 and
and 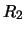 are divided by an arc
are divided by an arc 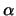 such that the normal to
such that the normal to 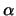 points from
points from
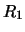 to
to 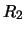 , and let
, and let
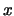 be a color of
be a color of 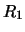 . Then the color of
. Then the color of 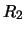 is required to be
is required to be
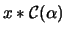 .
At a crossing, there are four regions. There is a unique region among the four
from which all the normals of the arcs point to other regions.
Such a region is called the source region at a crossing.
.
At a crossing, there are four regions. There is a unique region among the four
from which all the normals of the arcs point to other regions.
Such a region is called the source region at a crossing.
Figure:
Quandle colorings of regions
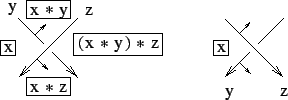 |
In Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) , it is seen that colorings of regions
(region colors) are well-defined.
In the left of the figure, a positive crossing is depicted. There are two ways
to go from the source region (leftmost region)
to the rightmost region, through upper arcs and lower arcs.
Through upper arcs we obtain the color
, it is seen that colorings of regions
(region colors) are well-defined.
In the left of the figure, a positive crossing is depicted. There are two ways
to go from the source region (leftmost region)
to the rightmost region, through upper arcs and lower arcs.
Through upper arcs we obtain the color 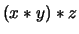 ,
and through the lower arcs
,
and through the lower arcs
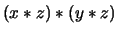 , that coincide by a quandle condition.
The triple
, that coincide by a quandle condition.
The triple 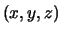 is called the ordered triple of colors at the crossing.
The situation is similar at a negative crossing (the right of Fig.
is called the ordered triple of colors at the crossing.
The situation is similar at a negative crossing (the right of Fig. ![[*]](file:/usr/share/latex2html/icons/crossref.png) .
The triple
.
The triple 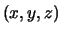 is called the ordered triple of colors at the crossing.
Specifically,
is called the ordered triple of colors at the crossing.
Specifically, 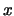 is the color of the source region,
is the color of the source region, 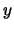 is the color of the under-arc
from which the normal of the over-arc points, and
is the color of the under-arc
from which the normal of the over-arc points, and 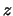 is the color of the over-arc.
is the color of the over-arc.



Next: -Cocycle invariants
Up: Definitions
Previous: Colorings of knot diagrams
Masahico Saito - Quandle Website
2005-09-29
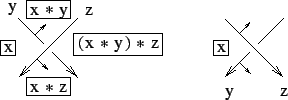
![]() , it is seen that colorings of regions
(region colors) are well-defined.
In the left of the figure, a positive crossing is depicted. There are two ways
to go from the source region (leftmost region)
to the rightmost region, through upper arcs and lower arcs.
Through upper arcs we obtain the color
, it is seen that colorings of regions
(region colors) are well-defined.
In the left of the figure, a positive crossing is depicted. There are two ways
to go from the source region (leftmost region)
to the rightmost region, through upper arcs and lower arcs.
Through upper arcs we obtain the color ![]() ,
and through the lower arcs
,
and through the lower arcs
![]() , that coincide by a quandle condition.
The triple
, that coincide by a quandle condition.
The triple ![]() is called the ordered triple of colors at the crossing.
The situation is similar at a negative crossing (the right of Fig.
is called the ordered triple of colors at the crossing.
The situation is similar at a negative crossing (the right of Fig. ![]() .
The triple
.
The triple ![]() is called the ordered triple of colors at the crossing.
Specifically,
is called the ordered triple of colors at the crossing.
Specifically, ![]() is the color of the source region,
is the color of the source region, ![]() is the color of the under-arc
from which the normal of the over-arc points, and
is the color of the under-arc
from which the normal of the over-arc points, and ![]() is the color of the over-arc.
is the color of the over-arc.