The cocycle invariant for classical knots [CJKLS03] using quandle ![]() -cocycles
was defined as follows.
Let
-cocycles
was defined as follows.
Let ![]() be a finite quandle and
be a finite quandle and ![]() an abelian group.
an abelian group.
A function
![]() is called a quandle
is called a quandle ![]() -cocycle
if it satisfies the
-cocycle
if it satisfies the ![]() -cocycle condition
-cocycle condition
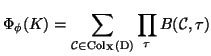
The value (an element of
![]() ) of the invariant is written as
) of the invariant is written as
![]() ,
so that if
,
so that if
![]() , the value is written as
a polynomial
, the value is written as
a polynomial
![]() .
The fact that
.
The fact that
![]() is a knot invariant is proved easily by checking
Reidemeister moves [CJKLS03].
For example, in Fig.
is a knot invariant is proved easily by checking
Reidemeister moves [CJKLS03].
For example, in Fig. ![]() of Chapter
of Chapter ![]() ,
the product of weights that appear in the LHS
is
,
the product of weights that appear in the LHS
is
![]() from the top to bottom crossings,
and for the RHS it is
from the top to bottom crossings,
and for the RHS it is
![]() , and the equality obtained is exactly
the
, and the equality obtained is exactly
the ![]() -cocycle condition in multiplicative notation, after canceling
-cocycle condition in multiplicative notation, after canceling
![]() .
.
The cocycle invariant can be also written as a family (multi-set, a set with repetition allowed) of weight sums [Lop03]
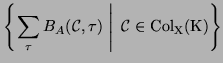
The ![]() -cocycle invariant is well-defined for virtual knots, as checked in
a similar manner.
-cocycle invariant is well-defined for virtual knots, as checked in
a similar manner.
Let
![]() , an Alexander quandle as
, an Alexander quandle as ![]() and an abelian group
as
and an abelian group
as ![]() , and put the source colors
, and put the source colors ![]() , for example, at the top crossing.
This color vector goes down to the next crossing, giving
, for example, at the top crossing.
This color vector goes down to the next crossing, giving
![]() ,
,
![]() =
=![]() , and comes back to
, and comes back to
![]() , by the coloring rule, and defines a non-trivial
coloring
, by the coloring rule, and defines a non-trivial
coloring
![]() .
In fact any pair extends to a coloring,
and
.
In fact any pair extends to a coloring,
and
![]() .
.
Consider the function
![]() defined by
defined by
![]() . Then this satisfies the
. Then this satisfies the ![]() -cocycle condition
by calculation (we will further discuss this method of construction
of
-cocycle condition
by calculation (we will further discuss this method of construction
of ![]() -cocycles later).
-cocycles later).
The contribution is computed by
We make the following notational convention.
In the above example, if we denote additive generators ![]() and
and ![]() multiplicatively by
multiplicatively by ![]() and
and ![]() , then the elements of
, then the elements of ![]() in multiplicative notation
are written as
in multiplicative notation
are written as
![]() . Hence the invariant in the state-sum form
is written as
. Hence the invariant in the state-sum form
is written as
![]() . In Maple calculations,
it is convenient and easier to see outputs if we use the symbols
. In Maple calculations,
it is convenient and easier to see outputs if we use the symbols
![]() and
and ![]() for
for ![]() and
and ![]() . Then the additive notations
remain on superscripts and the addition is also retained in exponents
(
. Then the additive notations
remain on superscripts and the addition is also retained in exponents
(
![]() ). With this convention the invariant value
is written as
). With this convention the invariant value
is written as
![]() .
We use this notation if there is no confusion.
.
We use this notation if there is no confusion.