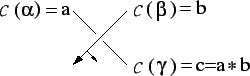 |
Let
![]() denote the set of colorings of a knot diagram
denote the set of colorings of a knot diagram ![]() of a knot
of a knot ![]() by a quandle
by a quandle ![]() .
It is known [FR92], and can be checked on diagrams,
that for any coloring
.
It is known [FR92], and can be checked on diagrams,
that for any coloring
![]() of a diagram
of a diagram ![]() of a knot
of a knot ![]() by a quandle
by a quandle ![]() ,
there is a unique coloring
,
there is a unique coloring
![]() of a
diagram
of a
diagram ![]() of the same knot
of the same knot ![]() that is obtained from
that is obtained from ![]() by a single
Reidemeister move of any type (I, II, or III),
such that the colorings coincide outside of a small portion of the diagrams
where the move is performed.
Thus there is a one-to-one correspondence between the sets of colorings
of two diagrams of the same knot.
In particular, the cardinality
by a single
Reidemeister move of any type (I, II, or III),
such that the colorings coincide outside of a small portion of the diagrams
where the move is performed.
Thus there is a one-to-one correspondence between the sets of colorings
of two diagrams of the same knot.
In particular, the cardinality
![]() is a knot invariant.
Note that any knot diagram is colored by a single element of a given quandle.
Such a monochromatic coloring is called trivial.
Hence for any knot
is a knot invariant.
Note that any knot diagram is colored by a single element of a given quandle.
Such a monochromatic coloring is called trivial.
Hence for any knot ![]() and any quandle
and any quandle ![]() ,
,
![]() is at least
the cardinality
is at least
the cardinality ![]() of the quandle.
of the quandle.
In fact, the Reidemeister moves I, II, III correspond to
the quandle axiom I, II, III, respectively. In particular,
a type III move represents the self-distributivity as depicted in Fig. ![]() .
.
A coloring is defined for virtual knot diagrams in a completely similar manner, and the sets of colorings of two virtual diagrams of the same virtual knot are in one-to-one correspondence, as checked by Reidemeister moves for virtual knots.
For a coloring
![]() of a knot diagram
of a knot diagram ![]() ,
there is a coloring of regions ([FRS95,FRS*])
that extend
,
there is a coloring of regions ([FRS95,FRS*])
that extend
![]() as depicted in Fig.
as depicted in Fig. ![]() .
The set
.
The set
![]() of regions is defined to be the
set of connected components of the complement of
(underlying) projection of a knot diagram in
of regions is defined to be the
set of connected components of the complement of
(underlying) projection of a knot diagram in
![]() (or
(or
![]() ).
A coloring of regions is an assignment of quandle elements to regions,
together with a given coloring
).
A coloring of regions is an assignment of quandle elements to regions,
together with a given coloring
![]() of arcs,
of arcs,
![]() ,
,
![]() ,
that satisfies the following requirement: Suppose the two regions
,
that satisfies the following requirement: Suppose the two regions ![]() and
and ![]() are divided by an arc
are divided by an arc ![]() such that the normal to
such that the normal to ![]() points from
points from
![]() to
to ![]() , and let
, and let
![]() be a color of
be a color of ![]() . Then the color of
. Then the color of ![]() is required to be
is required to be
![]() .
The set of colorings
.
The set of colorings
![]() of arcs and regions is denoted by
of arcs and regions is denoted by
![]() .
.
In Fig. ![]() , it is seen that a coloring of regions
(region colors) are well-defined near a crossing.
In the left of the figure, a positive crossing is depicted.
Near a crossing, there are four regions, one of which is a unique region
from which all the normal vectors of the arcs point to other regions.
Such a region is called the source region at a crossing.
There are two ways
to go from the source region (leftmost region)
to the rightmost region, through upper arcs and lower arcs.
Through upper arcs we obtain the color
, it is seen that a coloring of regions
(region colors) are well-defined near a crossing.
In the left of the figure, a positive crossing is depicted.
Near a crossing, there are four regions, one of which is a unique region
from which all the normal vectors of the arcs point to other regions.
Such a region is called the source region at a crossing.
There are two ways
to go from the source region (leftmost region)
to the rightmost region, through upper arcs and lower arcs.
Through upper arcs we obtain the color ![]() ,
and through the lower arcs
,
and through the lower arcs
![]() , that coincide by the self-distributivity
of a quandle.
The situation is similar at a negative crossing (the right of Fig.
, that coincide by the self-distributivity
of a quandle.
The situation is similar at a negative crossing (the right of Fig. ![]() ,
the colors of the regions unspecified are for an exercise).
The triple of elements
,
the colors of the regions unspecified are for an exercise).
The triple of elements ![]() of
of ![]() is called the source colors or ordered triple of colors at the crossing.
Specifically,
is called the source colors or ordered triple of colors at the crossing.
Specifically, ![]() is the color of the source region,
is the color of the source region, ![]() is the color of the under-arc
from which the normal of the over-arc points, and
is the color of the under-arc
from which the normal of the over-arc points, and ![]() is the color of the over-arc
(the pair
is the color of the over-arc
(the pair ![]() is the source colors of arcs).
is the source colors of arcs).
For any coloring
![]() of a knot diagram
of a knot diagram ![]() on
on
![]() (or
(or
![]() ) by a quandle
) by a quandle ![]() ,
and any specific choice of a color
,
and any specific choice of a color ![]() for a region
for a region
![]() ,
there is a unique region coloring
,
there is a unique region coloring
![]() that extends
that extends
![]() ,
,
![]() ,
such that
,
such that
![]() .
This is seen as follows.
Let
.
This is seen as follows.
Let
![]() and take a path
and take a path ![]() from
from ![]() to
to ![]() that avoids crossings of
that avoids crossings of ![]() and intersects transversely in finite points with
and intersects transversely in finite points with ![]() . Along
. Along
![]() the element
the element
![]() is determined by the coloring rule
of regions from the colors of arcs.
Take two paths,
is determined by the coloring rule
of regions from the colors of arcs.
Take two paths, ![]() and
and ![]() , from
, from ![]() to
to ![]() ,
that miss crossing points.
There is a homotopy from
,
that miss crossing points.
There is a homotopy from
![]() to
to ![]() , and it is assumed without loss of generality
that during the homotopy the paths experience, themselves and in
relation the the knot projection, a sequence of Reidemeister moves.
In particular, when a path goes through a crossing of the knot projection,
it corresponds to a type III move, and well-definedness
under such a move is checked in Fig.
, and it is assumed without loss of generality
that during the homotopy the paths experience, themselves and in
relation the the knot projection, a sequence of Reidemeister moves.
In particular, when a path goes through a crossing of the knot projection,
it corresponds to a type III move, and well-definedness
under such a move is checked in Fig. ![]() .
Therefore the color of regions are uniquely determined by a color of a single
region.
Note that we used the fact that the plane is simply connected,
i.e., any two paths are homotopic.
In general, we cannot
define region colors for knots on a surface, or virtual knots.
.
Therefore the color of regions are uniquely determined by a color of a single
region.
Note that we used the fact that the plane is simply connected,
i.e., any two paths are homotopic.
In general, we cannot
define region colors for knots on a surface, or virtual knots.