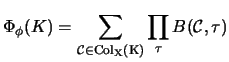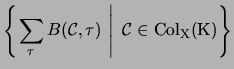Next: -Cocycle invariants
Up: Definitions
Previous: Colorings of regions
The cocycle invariant for classical knots [CJKLS03] using quandle 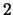 -cocycles
was defined as follows.
Let
-cocycles
was defined as follows.
Let 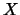 be a finite quandle and
be a finite quandle and 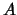 an abelian group, typically a finite cyclic
group
an abelian group, typically a finite cyclic
group
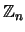 ,
,
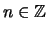 ,
, 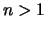 .
.
A function
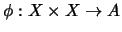 is called a quandle
is called a quandle 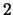 -cocycle if it satisfies the
-cocycle if it satisfies the 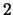 -cocycle condition
-cocycle condition
and
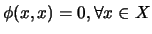 .
Let
.
Let 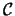 be a coloring of a given knot diagram
be a coloring of a given knot diagram 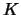 by
by 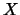 .
The Boltzmann weight
.
The Boltzmann weight
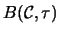 at a crossing
at a crossing 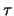 of
of 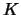 is then defined by
is then defined by
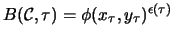 ,
where
,
where 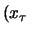 ,
, 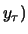 is the ordered pair of colors at
is the ordered pair of colors at 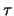 and
and
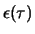 is the sign (
is the sign (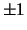 ) of
) of 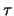 .
Here
.
Here
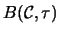 is an element of
is an element of 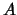 written multiplicatively.
The formal sum (called a state-sum) in the group ring
written multiplicatively.
The formal sum (called a state-sum) in the group ring
![$ \mathbb{Z}[A]$](img88.png) is called the quandle
is called the quandle 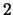 -cocycle invariant.
A value (an element of
-cocycle invariant.
A value (an element of
![$ \mathbb{Z}[A]$](img88.png) ) is written as
) is written as
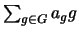 ,
so that if
,
so that if
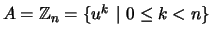 , a value is written as
a polynomial
, a value is written as
a polynomial
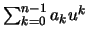 .
That
.
That
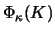 is a knot invariant is proved easily by checking
Reidemeister moves [CJKLS03].
is a knot invariant is proved easily by checking
Reidemeister moves [CJKLS03].
The cocycle invariant can be also written as
a family (multi-set, a set with repetition allowed) of weight sums [Lop03]
where now the values of 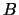 in
in 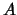 are denoted by additive notation.
Then this is well-defined for any quandle of any cardinality.
are denoted by additive notation.
Then this is well-defined for any quandle of any cardinality.



Next: -Cocycle invariants
Up: Definitions
Previous: Colorings of regions
Masahico Saito - Quandle Website
2005-09-29
![]() is called a quandle
is called a quandle ![]() -cocycle if it satisfies the
-cocycle if it satisfies the ![]() -cocycle condition
-cocycle condition