Invariants for knotted surfaces

A diagram of knotted surfaces in $4$-space is defined in a similar manner as classical knot diagrams. A projection of a surface embedded in $4$-space to $3$-space has, locally, embedded sheets, double point curves, isolated branch points and triple points. According to crossing information along the double curves, under-sheets are broken. See [CKS00,CarSai98a] for details.

We specify the orientation of a knotted surface diagram by orientation normal vectors to broken sheets. A coloring for a knotted surface diagram $D$ by a quandle $X$ is an assignment of an element (called a color) of a quandle $X$ to each broken sheet such that $p*q=r$ holds at every double point, where $p$ (or $r$, respectively) is the color of the under-sheet behind (or in front of) the over-sheet with the color $q$, where the normal of the over-sheet points from the under-sheet behind it to the front. The pair $(p,q)\in X\times X$ is called the color of the double point. The property whether a knotted surface $K$ admits a non-trivial coloring or not is independent of the particular choice of a diagram of $K$. The coloring rule is depicted in Fig. .

Figure: Colors at double curves and $3$-cocycle at a triple point

For a fixed finite quandle $X$ and a $3$-cocycle $\theta$, we define a knotted surface invariant as follows: Let $K$ be a knotted surface diagram and let ${\cal C} : {\cal R} \rightarrow X$ be a coloring of $K$, where ${\cal R}$ is the set of sheets of $K$. Recall that a function $\theta : X \times X \times X \rightarrow A$ is a quandle $3$-cocycle if, for any $p,q,r, s \in X$,

$${ \theta (p,r,s) +\theta(p*r,q*r,s) +\theta(p,q,r) }$$

$$= \theta(p*q,r, s) + \theta(p,q,s) + \theta(p*s,q*s,r*s),$$

and $\theta(p,p,q) = 0$, $\theta(p,q,q) = 0$. The Boltzman weight at a triple point $\tau$ is defined by $B(\tau, {\cal C}) = \theta(x,y,z)^{\epsilon (\tau)},$ where $\epsilon(\tau)$ is the sign of the triple point $\tau$ (see [CarSai98a]), and $x, y, z$ are the colors of the bottom, middle, and top sheets, respectively, around the source region of $\tau$. The source region is the region from which normals of top, middle and bottom sheets point. In the right of Fig. , the triple point $\tau$ is positive, so that $B(\tau, {\cal C})=\theta(p,q,r)$. The state-sum is defined by

$$\Phi(K)= \sum_{{\cal C}} \prod_{\tau} B( \tau, {\cal C}).$$

it was shown in [CJKLS03] that $\Phi(K)$ is an invariant, called the $($quandle$)$ cocycle invariant of knotted surfaces.

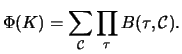
The value of the state-sum invariant depends only on the cohomology class represented by the defining cocycle [CJKLS03] for both classical knots and knotted surfaces.