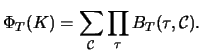In [CES02], a cocycle invariant using twisted quandle
cohomology theory was defined.
Let ![]() be a quandle, and
be a quandle, and ![]() be an Alexander quandle with variable
be an Alexander quandle with variable ![]() (typically
(typically
![]() for a prime
for a prime ![]() and a polynomial
and a polynomial ![]() ).
A function
).
A function
![]() is called a twisted quandle
is called a twisted quandle ![]() -cocycle if it satisfies
the twisted
-cocycle if it satisfies
the twisted ![]() -cocycle condition
-cocycle condition
Let ![]() be an oriented knot diagram with orientation normal vectors.
The underlying projection of the
diagram divides the
be an oriented knot diagram with orientation normal vectors.
The underlying projection of the
diagram divides the ![]() -space into regions.
For a crossing
-space into regions.
For a crossing ![]() , among four regions adjacent to
, among four regions adjacent to ![]() ,
there is a unique region
,
there is a unique region ![]() such that all normal vectors of arcs near
such that all normal vectors of arcs near ![]() point from
point from ![]() to other regions. Such a region
to other regions. Such a region ![]() is called
the source region of
is called
the source region of ![]() .
Take an oriented arc
.
Take an oriented arc ![]() from the region at infinity to
a region
from the region at infinity to
a region
![]() such that
such that ![]() intersects the
arcs (missing crossing points) of
the diagram transversely in finitely many points.
The Alexander numbering
intersects the
arcs (missing crossing points) of
the diagram transversely in finitely many points.
The Alexander numbering
![]() of a region
of a region ![]() is the number
of such intersections counted with signs.
If the orientation of
is the number
of such intersections counted with signs.
If the orientation of ![]() agrees with the normal vector of the arc
where
agrees with the normal vector of the arc
where ![]() intersects, then the intersection is positive
(counted as
intersects, then the intersection is positive
(counted as ![]() ), otherwise negative (counted as
), otherwise negative (counted as ![]() ).
The Alexander numbering
).
The Alexander numbering
![]() of a crossing
of a crossing ![]() is defined to be
is defined to be
![]() where
where ![]() is the source region of
is the source region of ![]() .
.
For a coloring ![]() of
of ![]() by
by ![]() , the twisted
, the twisted ![]() Boltzmann
Boltzmann![]() weight
at a triple point
weight
at a triple point ![]() is defined by
is defined by
![]() where
where ![]() is a twisted
is a twisted ![]() -cocycle,
and
-cocycle,
and
![]() is the sign of the crossing
is the sign of the crossing ![]() .
This is in multiplicative notation, so that the action of
.
This is in multiplicative notation, so that the action of ![]() on
on ![]() is written by
is written by ![]() .
The colors
.
The colors ![]() assigned near
assigned near ![]() are chosen in
the same manner as in the ordinary
are chosen in
the same manner as in the ordinary ![]() -cocycle invariant,
and
-cocycle invariant,
and
![]() is the Alexander numbering of
is the Alexander numbering of ![]() .
The twisted quandle
.
The twisted quandle ![]() -cocycle invariant
is the state-sum
-cocycle invariant
is the state-sum