


Next: Twisted cocycle invariants
Up: Definitions
Previous: -Cocycle invariants
We consider Alexander quandles and their quandle cocycles
with the coefficient group of the form
![$ X=\mathbb{Z}_p[t,t^{-1}]/h(t)=A$](img105.png) .
In this case some
.
In this case some 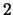 - and
- and 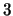 -cocycles are constructed by
polynomial functions. These constructions were given in [Mochi03].
-cocycles are constructed by
polynomial functions. These constructions were given in [Mochi03].
In general, functions of the form
are 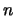 -cocycles for a variety of Alexander quandles mod
-cocycles for a variety of Alexander quandles mod 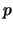 ,
where
,
where 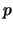 is a prime and
is a prime and 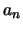 is either 0 or a power of
is either 0 or a power of 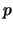 .
In our case, we used the following cocycles.
.
In our case, we used the following cocycles.
There is another type of 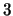 -cocycles Mochizuki constructed for dihedral quandles
-cocycles Mochizuki constructed for dihedral quandles 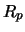 for prime
for prime 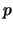 .
It is given by the formula
.
It is given by the formula
![$\displaystyle \theta (x,y,z)= (x-y) [(2 z^p - y^p) - (2z-y)^p ]/p$](img115.png)
mod
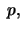
where the numerator computed in
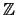 is divisible by
is divisible by 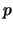 , and then after
dividing it by
, and then after
dividing it by 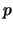 , the value is taken as an integer modulo
, the value is taken as an integer modulo 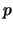 .
.



Next: Twisted cocycle invariants
Up: Definitions
Previous: -Cocycle invariants
Masahico Saito - Quandle Website
2005-09-29
![]() -cocycles Mochizuki constructed for dihedral quandles
-cocycles Mochizuki constructed for dihedral quandles ![]() for prime
for prime ![]() .
It is given by the formula
.
It is given by the formula