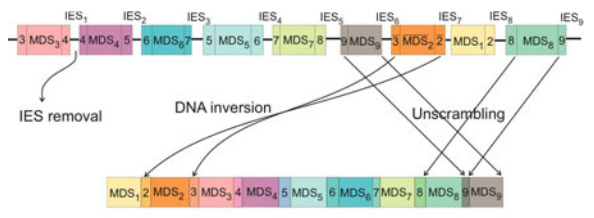
We introduce a model that describes rearrangement pathways of DNA recombination events. The recombination processes may happen in a succession, possibly with some recombination events performed simultaneously, but others in a prescribed order. These events are modeled by three rewriting rules applied on a set of formal linear and circular words. We define a partial order on these sets in such a way that two sets are related by this order when molecules represented by one are produced by recombination events from the molecules represented by the other. We apply our model to experimental data obtained for DNA rearrangement of actin I gene in O. triffalax ciliates, and we predict possible pathways of gene rearrangement compatible with the data.
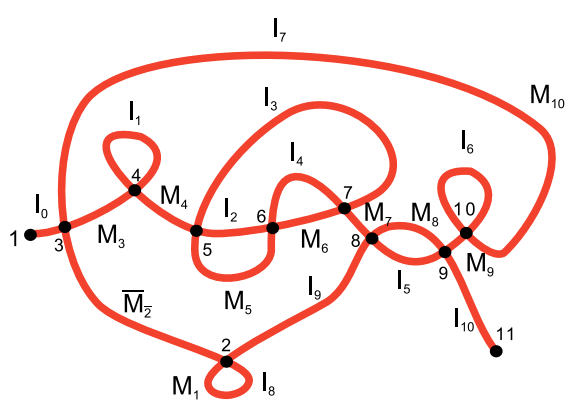
The paper reviews two computing models by DNA self-assembly whose proof of principal have recently been experimentally confirmed. The first model incorporates DNA nano-devices and triple cross-over DNA molecules to algorithmically arrange non DNA species. This is achieved by simulating a finite state automaton with output where golden nanoparticles are assembled to read-out the result. In the second model, a complex DNA molecule representing a graph emerges as a solution of a computational problem. This supports the idea that in molecular self-assembly computing it may be necessary to develop the notion of shape processing besides the classical approach through symbol processing.
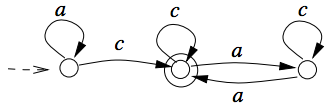
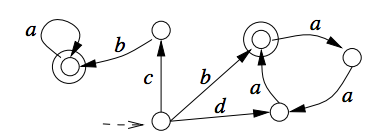
In spite of wide investigations of finite splicing systems in formal language theory, basic questions, such as their characterization, remain unsolved. In search for understanding the class of finite splicing systems, it has been conjectured that a necessary condition for a regular language L to be a splicing language is that L must have a constant in the Schützenberger's sense. We prove this longstanding conjecture to be true. The result is based on properties of strongly connected components of the minimal deterministic finite state automaton for a regular splicing language.
The paper is a short overview of a recent model of homologous DNA recombination events guided by RNA templates that have been observed in certain species of ciliates. This model uses spatial graphs to describe DNA rearrangements and show how gene recombination can be modeled as topological braiding of the DNA. We show that a graph structure, which we refer to as an assembly graph, containing only 1- and 4-valent rigid vertices can provide a physical representation of the DNA at the time of recombination. With this representation, 4-valent vertices correspond to the alignment of the recombination sites, and we model the actual recombination event as smoothing of these vertices.
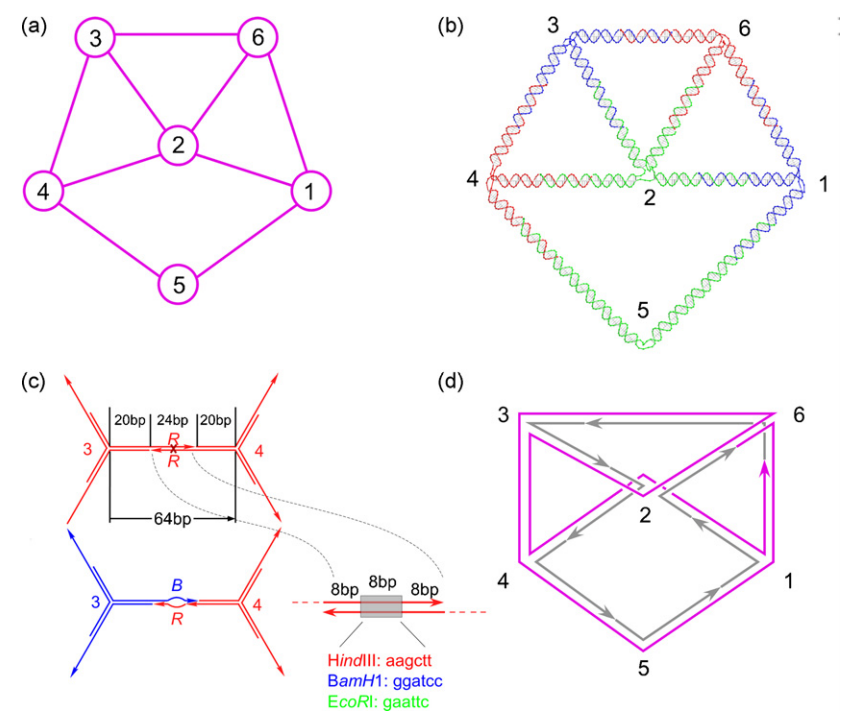
We demonstrate a computing method in which a DNA nano-object representing the solution of a problem emerges as a result of self-assembly. We report an experiment in which three-vertex colorability for a 6-vertex graph with 9 edges is solved by constructing a DNA molecule representing the colored graph itself. Our findings show that computation based on "shape processing" is a viable alternative to symbol processing when computing by molecular self-assembly.

Reciprocating devices are a key features in macroscopic machines. We have adapted the DNA PX-JX2 device to a reciprocal format. The PX-JX2 device is a robust sequence-dependent nanomachine, whose state of is established by a pair of control strands that set it to be either in the PX state or in the JX2 state. The two states differ by a half-turn rotation between their ends. Here we report the construction of a pair of reciprocal PX-JX2 devices, wherein the control strands leading to the PX state in one device lead to the JX2 state in the other device, and vice versa. The formation, transformation and reciprocal motions of these two device systems are confirmed using gel electrophoresis, and atomic force microscopy. This system is likely to be of use for molecular robotic applications where reciprocal motions are of value, in addition its inherent contribution to molecular choreography and molecular aesthetics.
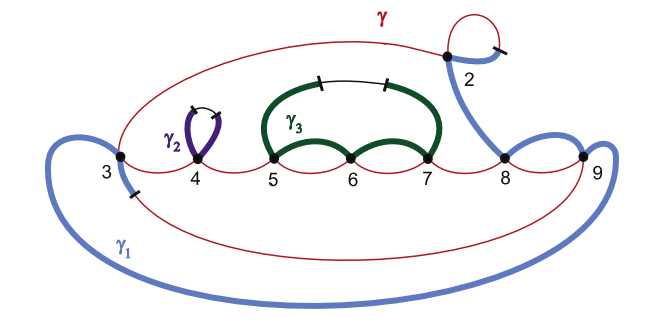
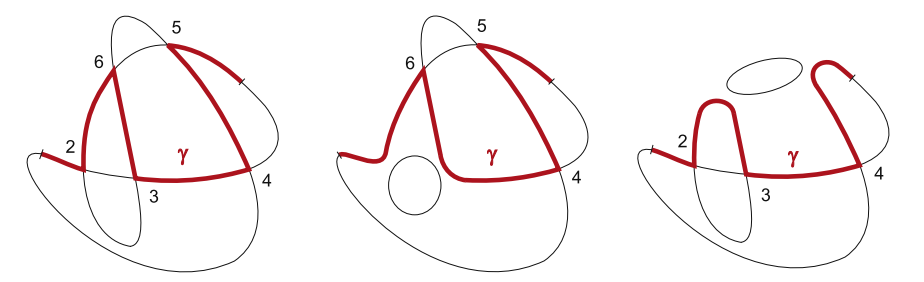
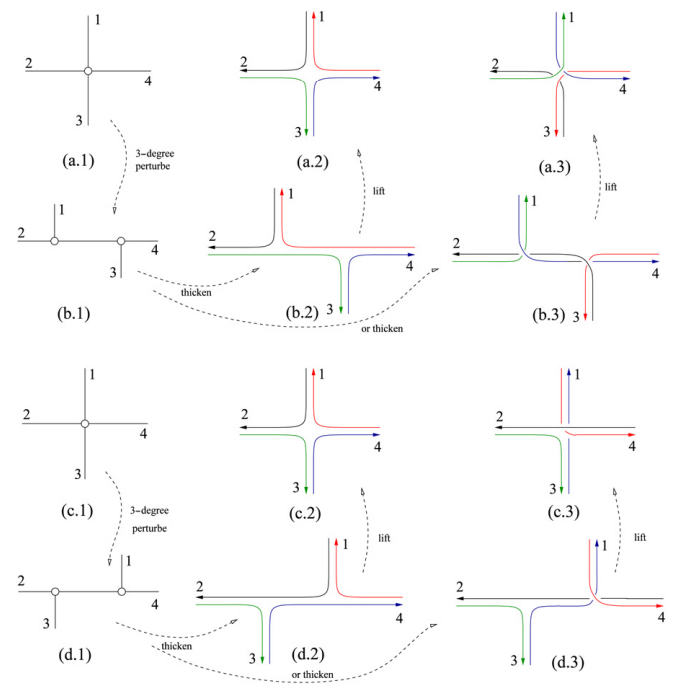
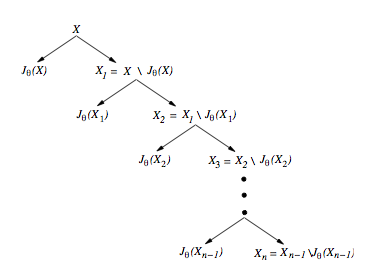
Motivated by DNA rearrangements and DNA homologous recombination modeled, we investigate smoothings on graphs that consist of only 4-valent and 1-valent rigid vertices, called assembly graphs. An assembly graph can be seen as a DNA representation of during certain recombination processes in which 4-valent vertices correspond to the alignment of the recombination sites. A single gene is modeled by a polygonal path in an assembly graph. A polygonal path makes a "right-angle" turn at every vertex, defining smoothings at the 4-valent vertices and therefore modeling the recombination process. We investigate minimal number of polygonal paths visiting all vertices of a given graph exactly once, and show that for every positive integer n there are graphs that require at least n such polygonal paths. We show that there is an embedding in three dimensional space of each assembly graph such that smoothings of vertices according to a given set of polygonal paths results in an unlinked graph. As some recombination processes may happen simultaneously, we characterize the subsets of vertices whose simultaneous smoothings keep a given gene in tact and give a characterization of all sequences of sets of vertices defining successive simultaneous smoothings that can realize complete gene rearrangement.
In this chapter we review several approaches and results in the computational study of gene assembly. We introduce the basic biological details of the gene assembly process as currently understood and experimentally observed. After mathematical preliminaries, we introduce two of the mostly studied molecular models for gene assembly (intermolecular and intramolecular) which are based on string rewriting techniques. We also discuss several mathematical approaches used in studying these models as well as some properties of the gene assembly process, called invariants, that hold independently of the molecular model and assembly strategy. Possible molecular implementation of the gene assembly process are presented through models for template-based DNA recombination.
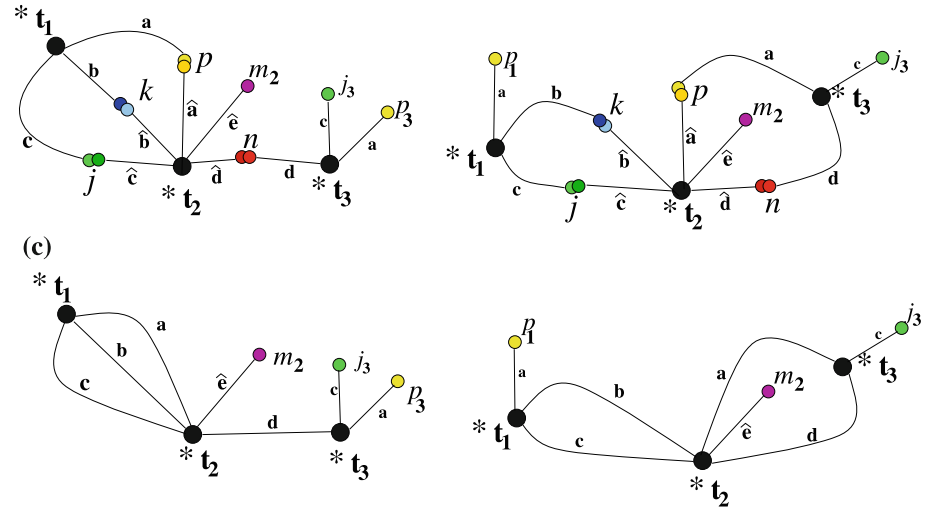
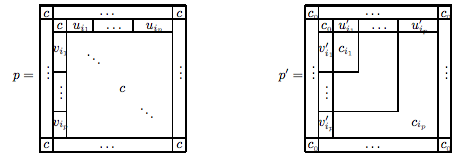
Given a set of flexible branched junction DNA molecules with sticky-ends (building blocks), called here "tiles", we consider the problem of determining the proper stoichiometry such that all sticky-ends could end up connected. In general, the stoichiometry is not uniform, and the goal is to determine the proper proportion (spectrum) of each type of molecule within a test tube to allow for complete assembly. According to possible components that assemble in complete complexes we partition multisets of tiles, called here "pots", into classes: unsatisfiable, weakly satisfiable, satisfiable and strongly satisfiable. This classification is characterized through the spectrum of the pot, and it can be computed in PTIME using the standard Gauss-Jordan elimination method. We also give a geometric description of the spectrum as a convex hull within the unit cube.
We consider a generalization of an Eulerian path in (multi)graphs. Define a pseudo Eulerian (multi)graph to be a (multi)graph which contains a path that visits each edge once or twice, if an edge is visited twice, then this is done in opposite directions. We show that every multigraph is pseudo-Eulerian. This shows that every multigraph can be assembled by DNA such that there is a single strand that traces each edge in the graph at least once.
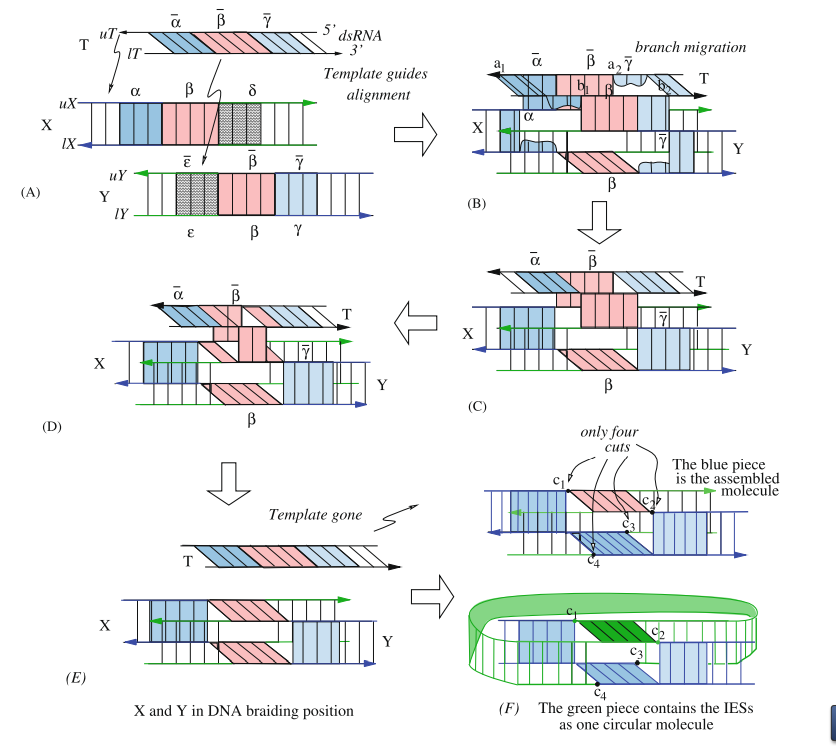
We present a model for homologous DNA recombination events guided by double-stranded RNA (dsRNA) templates, and apply this model to DNA rearrangements in some groups of ciliates, such as Stylonychia or Oxytricha. In these organisms, differentiation of a somatic macronucleus from a germline micronucleus involves extensive gene rearrangement, which can be modeled as topological braiding of the DNA, with the template-guided alignment proceeding through DNA branch migration.We show that a graph structure, which we refer to as an assembly graph, containing only 1- and 4-valent vertices can provide a physical representation of the DNA at the time of recombination.With this representation, 4-valent vertices correspond to the alignment of the recombination sites, and we model the actual recombination event as smoothing of these vertices.
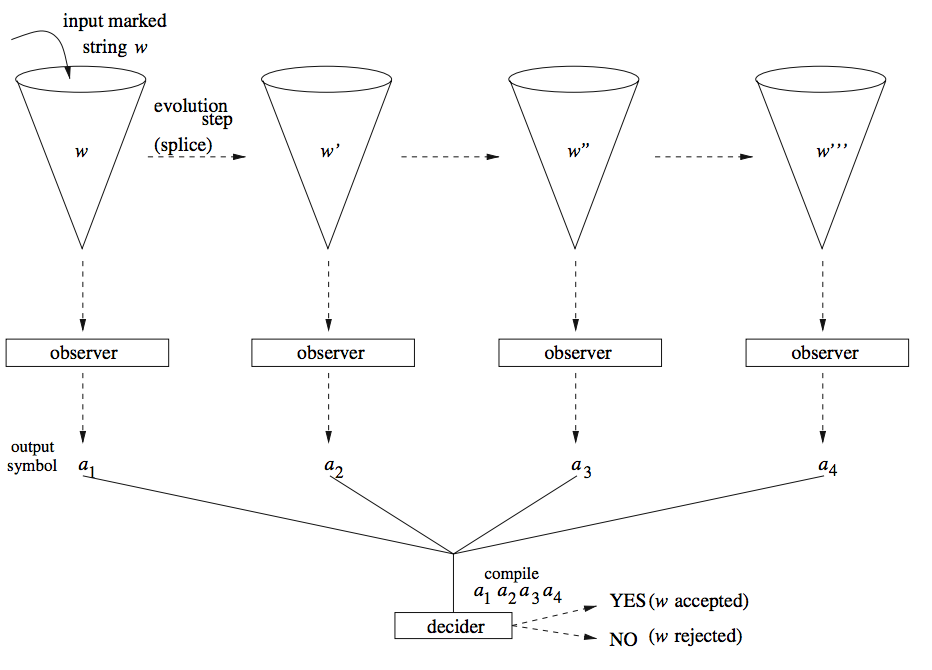
Motivated by several techniques for observing molecular processes in real-time we introduce a computing device that stresses the role of the observer in biological computations and that is based on the observed behavior of a splicing system. The basic idea is to introduce a marked DNA strand into a test tube with other DNA strands and restriction enzymes. Under the action of these enzymes the DNA starts to splice. An external observer monitors and registers the evolution of the marked DNA strand. The input marked DNA strand is then accepted if its observed evolution follows a certain expected pattern. We prove that using simple observers (finite automata), applied on finite splicing systems (finite set of rules and finite set of axioms), the class of recursively enumerable languages can be recognized.
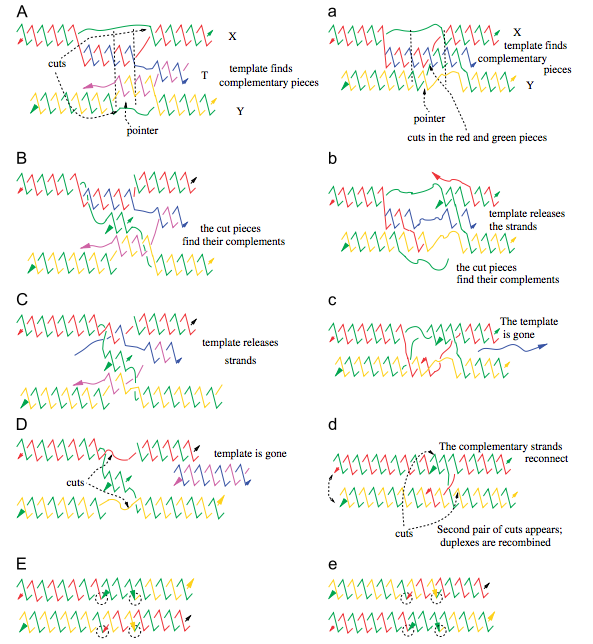
We propose molecular models for homologous DNA recombination events that are guided by either double-stranded RNA (dsRNA) or single-stranded RNA (ssRNA) templates. The models are applied to explain DNA rearrangements in some groups of ciliates, such as Stylonychia or Oxytricha, where extensive gene rearrangement occurs during differentiation of a somatic macronucleus from a germline micronucleus. We describe a model for RNA-template guided DNA recombination, such that the template serves as a catalyst that remains unchanged after DNA recombination. This recombination can be seen as topological braiding of the DNA, with the template-guided alignment proceeding through DNA branch migration. We show that a virtual knot diagram can provide a physical representation of the DNA at the time of recombination. Schematically, the braiding process can be represented as a crossing in the virtual knot diagram. The homologous recombination corresponds to removal of the crossings in the knot diagram (called smoothing). We show that if all recombinations are performed in parallel (i.e., parallel smoothings of the crossings) then one of the resulting DNA molecules will always contain all of the gene segments in their correct, linear order, which produces the mature DNA sequence.
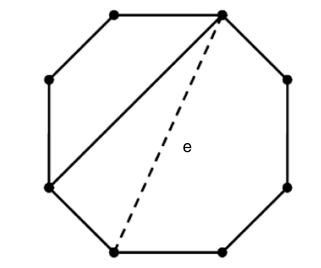
This paper introduces a way to define classes of graphs based on forbidding and enforcing boundary conditions. Forbidding conditions prevent a graph to have certain combinations of subgraphs and enforcing conditions impose certain subgraph structures. We say that a class of graphs is an fe-class if the class can be defined through forbidding and enforcing conditions. We investigate properties of fe-systems and characterize familiar classes of graphs such as paths and cycles, trees, bi-partite, complete, Eulerian, and k-regular graphs as fe-classes.
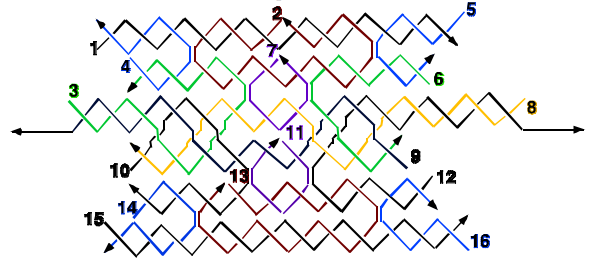
A transducer consists of an input/output alphabet, a finite set of states, and a transition function. From an input symbol applied to a given state, the transition function determines the next state, and an output symbol. Using DNA, we have constructed a transducer that divides a number by 3. The input consists of a series of individually addressable 2-state DNA nanomechanical devices that control the orientations of a group of flat 6-helix DNA motifs; these motifs have edge domains tailed in sticky ends corresponding to the numbers 0 and 1. Three-domain DNA molecules (TX tiles) act as computational tiles that correspond to the transitions that the transducer can undergo. The output domain of these TX tiles contains sticky ends that also correspond to 0 or 1. Two different DNA tiles can chelate these output domains: A 5 nm gold nanoparticle is attached to the chelating tile that binds to 0-domains and a 10 nm gold nanoparticle is attached to the chelating tile that binds to 1-domains. The answer to the division is represented by the series of gold nanoparticles, which can be interpreted as a binary number. The answers of the computation are read out by examination of the transducer complexes under a transmission electron microscope. The start or end points of the output sequence can be indicated by the presence of a 15 nm gold nanoparticle. This work demonstrates two previously unreported features integrated in a single framework: [1] a system that combines DNA algorithmic self-assembly with DNA nanomechanical devices that control that input, and [2] the arrangement of non-DNA species, here metallic nano-particles, through DNA algorithmic self-assembly. The nanomechanical devices are controlled by single-stranded DNA strands, allowing multiple input sequences to be applied to the rest of the system, thus guiding the algorithmic self-assembly to a variety of outputs.
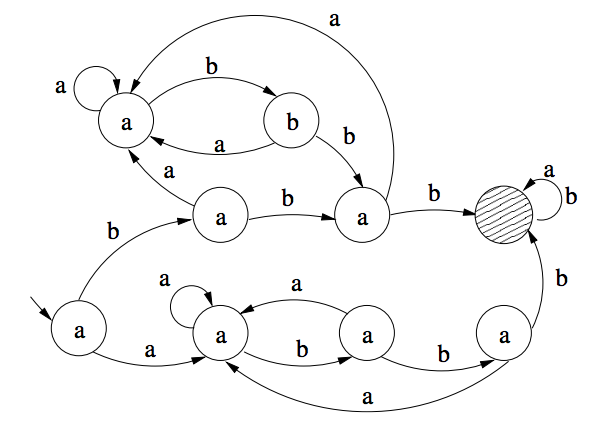
We initiate a study of one-dimensional cellular automata through two-dimensional languages. The time evolution of a bi-infinite configuration of a one-dimensional cellular automaton can be visualized as a half-plane array of symbols. The set of rectangular blocks extracted from such arrays forms a two-dimensional (picture) language. If this picture language is factorial-local, we call the cellular automaton factorial-local. We show that CA are factorial-local if and only if for sufficiently large k all their k-traces are shifts of finite type, and therefore are properly included in the class of regular cellular automata. We show that it is decidable whether a given set of blocks defines a factorial-local CA with a given radius, but the general membership problem for this class of cellular automata is undecidable.
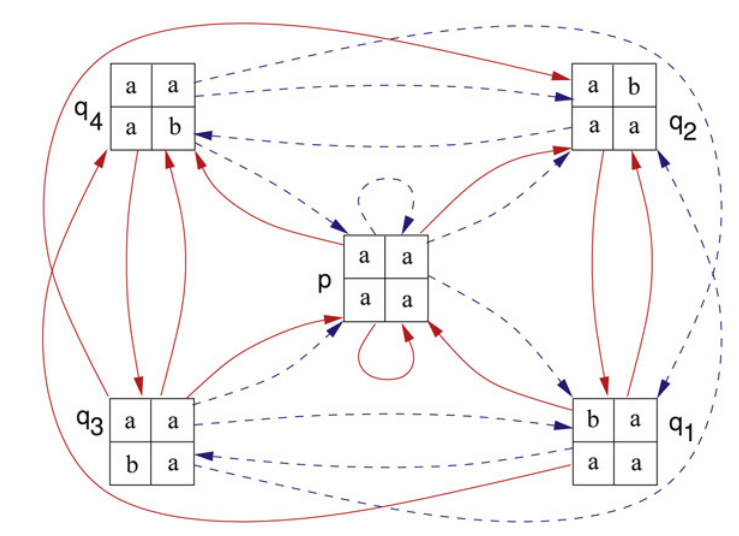
A new type of two-dimensional automaton has been defined to recognize a class of two-dimensional shifts of finite type having the property that every admissable block found within the related local picture language can be extended to a point of the subshift. Here it is shown that this automaton accurately represents the image of the represented two-dimensional shift of finite type under a block code. It is then shown that these automata can be used to check for a certain type of two-dimensional transitivity in the factor language of the corresponding shift space and how this relates to periodicity in the two-dimensional case. The paper closes with a notion of "follower sets" that are used to reduce the size of the automata representing two-dimensional sofic shifts.
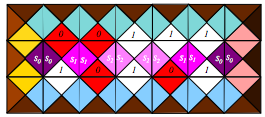
We consider sets of two-dimensional arrays, called here transducer generated languages, obtained by iterative applications of transducers (finite state automata with output). Each transducer generates a set of blocks of symbols such that the bottom row of a block is an input string accepted by the transducer and, by iterative application of the transducer, each row of the block is an output of the transducer on the preceding row. We show how these arrays can be implemented through molecular assembly of triple crossover DNA molecules. Such assembly could serve as a scaffold for arranging molecular robotic arms capable of simultaneous movements. We observe that transducer generated languages define a class of languages which is a proper subclass of recognizable picture languages, but it contains the class of all factorial local two-dimensional languages. By taking the average growth rate of the number of blocks in the language as a measure of its complexity, we further observe that arrays with high complexity patterns can be generated in this way.
Two-dimensional languages are nowadays a topic of interest for a lot of researchers in different frameworks. Actually the research follows two main directions. There are people interested in the tiling of the infinite plane and other ones more involved in the formal investigation of sets of finite two-dimensional blocks (or pictures), as a generalization of one-dimensional string languages. This paper has the ambition to bridge these two points of view, showing some similarities and differences. Differences arise since boundaries provide some information. Boundaries can limit or force the size and the content of pictures in a language. Furthermore, constraints fixed on a local language can considerably affect the ambiguity (i.e. number of pre-images) of its projection.
We consider two-dimensional languages, called here 2d transducer languages, generated by iterative applications of transducers (finite state automata with output). To each transducer a two-dimensional language consisting of blocks of symbols is associated: the bottom row of a block is an input string accepted by the transducer and, by iterative application of the transducer, each row of the block is an output of the transducer on the preceding row. We observe that this class of languages is a proper subclass of recognizable picture languages containing the class of all factorial local 2d languages. By taking the average growth rate of the number of blocks in the language as a measure of its complexity, also known as the entropy of the language, we show that every entropy value of a one-dimensional regular language can be obtained as an entropy value of a 2d transducer language.
As an emerging new research area, DNA nano engineering and computation, extends into other fields such as nanotechnology and material design, and is developing into a new sub-discipline of science and engineering. This chapter provides a brief overview of the design and development of computational devices by DNA. In particular two approaches for biomolecular models of automata are described. The first model is based on using action of restriction endonucleases and the second is based on DNA self-assembly and DNA nanomolecular devices.
We present a theoretical model for self-assembling DNA tiles with flexible branches. We encode an instance of a "problem" as a pot of such tiles for which a "solution" is an assembled complete complex without any free sticky ends. Using the number of tiles in an assembled complex as a measure of complexity we show how NTIME classes (such as NP and NEXP) can be represented with corresponding classes of the model.
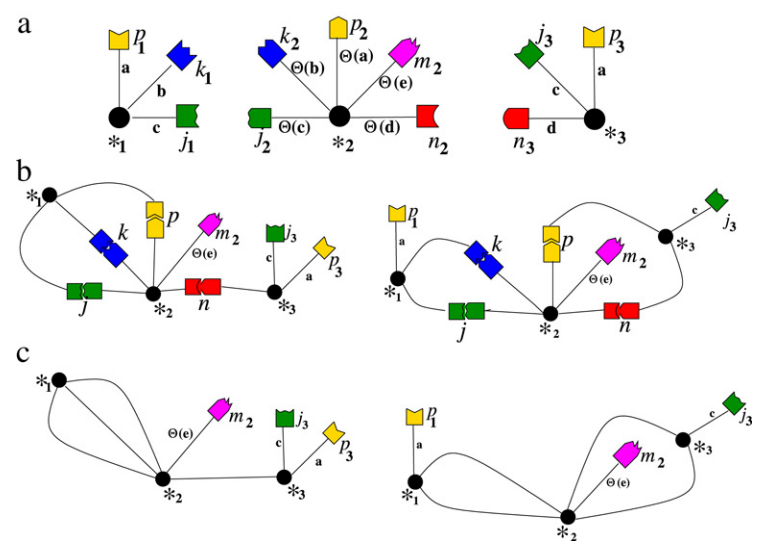
In this paper we study a generalization of the classical notions of solid codes and comma-free codes motivated by DNA based computing. This research extends the study of coding properties of DNA languages suitable for computations ,i.e., properties that ensure that no unintended Watson-Crick bonds are formed between the strings of the language. The mathematical formalization of the Watson-Crick binding between two DNA single strands is captured by the notion of an involution function: a function θ such that θ² equals the identity. An involution code refers to any of the generalizations of the classical notions of codes in which the identity function is replaced by an involution function. In this paper we study two such involution codes: θ-solid codes and θ-join codes. We investigate closure properties of these codes, as well as necessary conditions for θ-solid codes to be maximal. We also discuss the properties of codes that are themselves not θ-comma free but can be split into a union of subcodes that are θ-comma free.
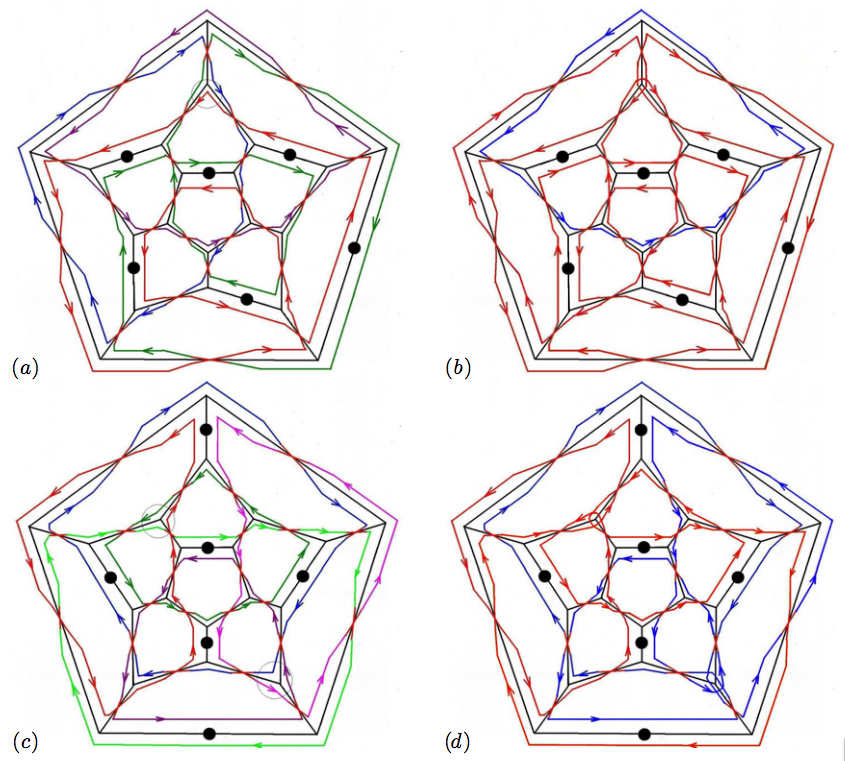
Cage structures engineered from nucleic acids are of interest in nanotechnology, for example as a means of drug delivery (Destito et al 2007). Until now, most experimentally realized DNA cages have crystallographic symmetry, such as the shape of a cube (Chen and Seeman 1991 Nature 350 631-3), a tetrahedron (Goodman et al 2005 Science 310 1661-5), an octahedron (Shih et al 2004 Nature 427 618-21) or a truncated octahedron (Zhang and Seeman 1994 J. Am. Chem. Soc. 116 1661-9). Two examples of cages with non-crystallographic symmetry, a dodecahedron and a buckyball, have been realized recently (He et al 2008 Nature 452 198-201). A characteristic feature of these realizations is the fact that the cages are built from a number of identical building blocks called tiles: 20 for the case of the dodecahedron, and 60 for the case of the buckyball. We derive here a blueprint for the organization of nucleic acid in a dodecahedral cage such that the final product has a minimal number of strands. In particular, we show that a dodecahedral cage can be realized in terms of only two circular DNA molecules. We focus on the dodecahedral cage, because the volume to surface ratio of such a cage is larger than that of its crystallographic counterparts given the same fixed radial distance of the polyhedral vertices from the centre of the structure, whilst still requiring a smaller complexity than the truncated icosahedron (buckyball). We therefore expect that the dodecahedral DNA cages discussed here may be of interest in further applications in nanotechnology.
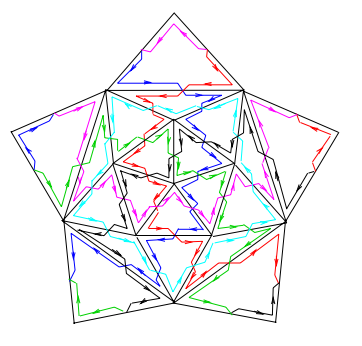
Blueprints of polyhedral cages with icosahedral symmetry made of circular DNA molecules are provided. The basic rule is that every edge of the cage is met twice in opposite directions by the DNA strand, and vertex junctions are realized by a set of admissible junction types. As nanocontainers for cargo storage and delivery, the icosidodecahedral cages are of special interest as they have the largest volume per surface ratio of all cages discussed here.
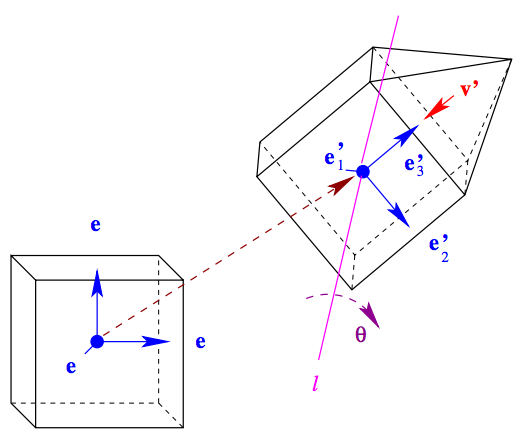
We outline an algebraic model for describing complex structures obtained through self-assembly of molecular building blocks and show that, with this model, the assembled structure can be associated to a language and it can be determined up to congruence.
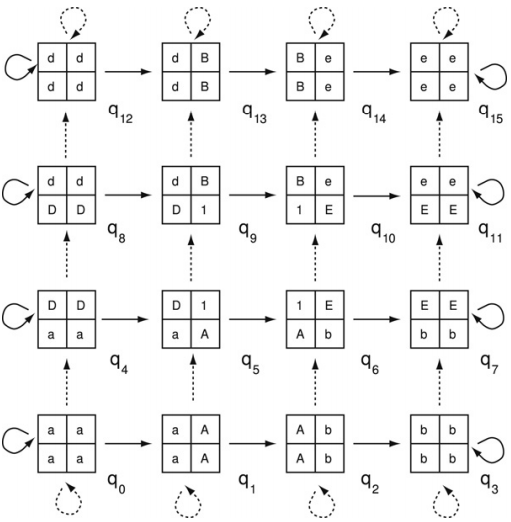
We employ a two-dimensional automaton to recognize a class of two-dimensional shifts of finite type having the property that every admissable block found within the related local picture language can be extended to a point of the subshift. Here, we show that the automaton accurately represents the image of the represented two-dimensional shift of finite type under a block code. We further show that such automata can be used to check for a certain type of two-dimensional transitivity in the factor language of the corresponding shift space and how this relates to periodicity in the two-dimensional case. The paper closes with a notion of "follower sets" used to reduce the size of the automata representing two-dimensional sofic shifts.
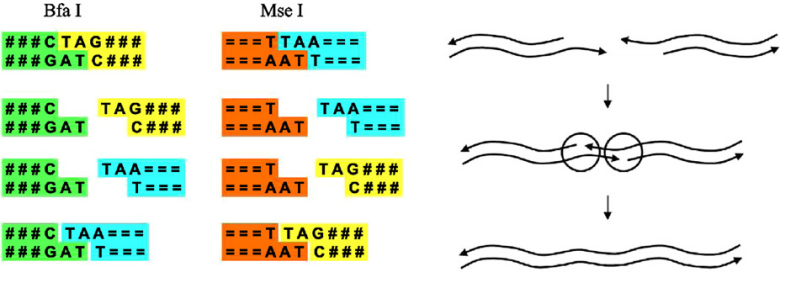
This paper introduces a new way of modeling classes of physical and biochemical processes and structures based on boundary conditions that are called "forbidden" and "enforced". The model of forbidding-enforcing systems (fe-systems) is presented in a general categorical sense and we use three specific examples of categories to illustrate three different phenomena. The hydrogen and covalent bonds of DNA, as well as, splicing DNA by enzymes, and recombination is illustrated with fe-systems on the category of languages (1-dimensional structures). Fe-systems over the simple category on sets can define the solutions to a computational problem, the k-colorability problem (information processing). By using the category of graphs fe-systems model graphs as an abstraction of 3-D structures such that a characterization of familiar classes of graphs, such as trees, bi-partite graphs, and complete graphs are obtained.