



Next: Quandle Cocycle Invariants with
Up: Quandle Cocycle Invariants of
Previous: Quandle -Cocycle Invariants of
Contents
To actually compute the quandle cocycle invariants from the definition, we need
to have an explicit cocycles.
In this section, we present quandle cocycles of Alexander quandles
written by polynomials,
called polynomial  quandle
quandle cocycles,
that can be used for such explicit calculations of the invariant.
Such cocycles were first constructed in [Mochi03],
and studied in [Ame06,Mochi05].
They have been extensively used in applications.
The following formulas are found in [Ame06].
cocycles,
that can be used for such explicit calculations of the invariant.
Such cocycles were first constructed in [Mochi03],
and studied in [Ame06,Mochi05].
They have been extensively used in applications.
The following formulas are found in [Ame06].
-
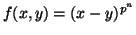 is a
is a 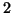 -cocycle for any Alexander quandle mod
-cocycle for any Alexander quandle mod 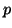 .
.
-
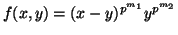 is a
is a 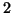 -cocycle for an
Alexander quandle
-cocycle for an
Alexander quandle
![$ \mathbb{Z}_p[t, t^{-1}]/g(t)$](img231.png) if
if 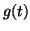 divides
divides
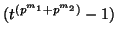 .
.
-
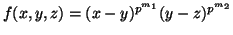 is a
is a 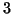 -cocycle for any Alexander quandle mod
-cocycle for any Alexander quandle mod 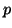 .
.
-
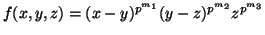 is a
is a 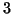 -cocycle for an
Alexander quandle
-cocycle for an
Alexander quandle
![$ \mathbb{Z}_p[t, t^{-1}]/g(t)$](img231.png) if
if 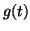 divides
divides
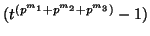 .
.
More general formula for 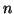 -cocycles are given in [Ame06].
We cite (a slightly simplified version of) her result:
-cocycles are given in [Ame06].
We cite (a slightly simplified version of) her result:
Proposition 4.4 ([
Ame06])
Consider an Alexander quandle
![$ X=\mathbb{Z}_p[t,t^{-1}]/h(t)=A$](img237.png)
. Let
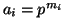
, for
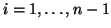
, where
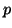
is a prime and
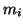
are non-negative integers. For a positive integer
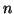
, let
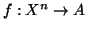
be defined by
Then
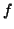
is an
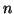
-cocycle
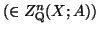
,
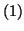
if
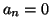
, or
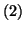
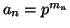
for a
positive integer
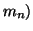
and
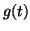
divides
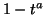
, where
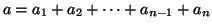
.
More specific polynomials and Alexander quandles considered are as follows.
Non-triviality of quandle cocycle invariants
for some of the cocycles below are obtained in [Ame06,StSm].
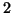 -cocycles:
-cocycles:
-
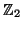 coefficients:
coefficients:
-
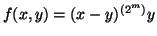 .
Alexander quandle
.
Alexander quandle
![$ \mathbb{Z}_2[t, t^{-1}]/(t^2+t+1)$](img253.png) has a non-trivial
has a non-trivial 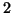 -cocycle
-cocycle
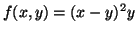 .
This
.
This 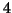 element quandle is well-known, and for example, isomorphic to the quandle consisting of
element quandle is well-known, and for example, isomorphic to the quandle consisting of 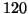 degree rotations of a regular tetrahedron. It is known to
have
degree rotations of a regular tetrahedron. It is known to
have 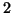 -dimensional cohomology group
-dimensional cohomology group
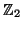 with
with
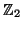 coefficient [CJKLS03]. The invariant values
for the coefficient
coefficient [CJKLS03]. The invariant values
for the coefficient
![$ \mathbb{Z}_2[t, t^{-1}]/(t^2+t+1)$](img253.png) are all of the form
are all of the form
![$ k[4 + 12u^{(t+1)}]$](img256.png) , so we conjecture that it is always the case. It is also an interesting problem to characterize this invariant.
, so we conjecture that it is always the case. It is also an interesting problem to characterize this invariant.
-
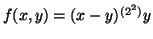 .
The quandle must be mod
.
The quandle must be mod 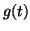 where
where 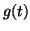 divides
divides 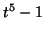 , but
, but
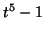 is factored into prime polynomials
is factored into prime polynomials
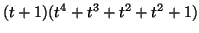 mod
mod 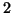 ,
so we set
,
so we set
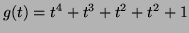 .
The Alexander quandle we use in this case, thus, is
.
The Alexander quandle we use in this case, thus, is
![$ \mathbb{Z}_2[t, t^{-1}]/(t^4+t^3+t^2+t+1)$](img261.png) with
with
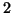 -cocycle:
-cocycle:
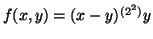 ,
which gives non-trivial invariants.
,
which gives non-trivial invariants.
-
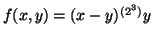 .
We factor
.
We factor 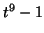 mod
mod 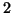 to
to
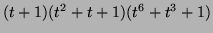 ,
so we try Alexander quandle
,
so we try Alexander quandle
![$ \mathbb{Z}_2[t, t^{-1}]/(t^6+t^3+1)$](img265.png) ,
which gives non-trivial invariants.
,
which gives non-trivial invariants.
-
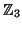 coefficients:
coefficients:
-
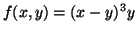 .
We have
.
We have
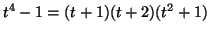 mod
mod 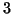 , so we try the quandle
, so we try the quandle
![$ \mathbb{Z}_3[t, t^{-1}]/(t^2+1)$](img269.png) which gives non-trivial invariants.
which gives non-trivial invariants.
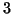 -cocycles:
-cocycles:
There is another type of 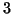 -cocycles Mochizuki constructed
specifically for dihedral quandles
-cocycles Mochizuki constructed
specifically for dihedral quandles 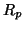 for prime
for prime 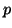 .
It is given by the formula
.
It is given by the formula
![$\displaystyle \theta (x,y,z)= (x-y) [(2 z^p - y^p) - (2z-y)^p ]/p$](img280.png)
mod
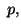
where the numerator computed in
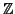 is divisible by
is divisible by 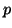 , and then after
dividing it by
, and then after
dividing it by 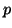 , the value is taken as an integer modulo
, the value is taken as an integer modulo 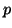 .
.




Next: Quandle Cocycle Invariants with
Up: Quandle Cocycle Invariants of
Previous: Quandle -Cocycle Invariants of
Contents
Masahico Saito - Quandle Website
2006-09-19
![]() quandle
quandle![]() cocycles,
that can be used for such explicit calculations of the invariant.
Such cocycles were first constructed in [Mochi03],
and studied in [Ame06,Mochi05].
They have been extensively used in applications.
The following formulas are found in [Ame06].
cocycles,
that can be used for such explicit calculations of the invariant.
Such cocycles were first constructed in [Mochi03],
and studied in [Ame06,Mochi05].
They have been extensively used in applications.
The following formulas are found in [Ame06].
![]() -cocycles are given in [Ame06].
We cite (a slightly simplified version of) her result:
-cocycles are given in [Ame06].
We cite (a slightly simplified version of) her result:
![]() ,
,
![]() .
.
![]() -cocycles Mochizuki constructed
specifically for dihedral quandles
-cocycles Mochizuki constructed
specifically for dihedral quandles ![]() for prime
for prime ![]() .
It is given by the formula
.
It is given by the formula