


Next: Bibliography
Up: Quandle Cocycle Invariants and
Previous: Realizing tangle embeddings
We use quandle cocycle invariants as obstructions to embedding tangles
in knots. To use the cocycle invariants, we first define cocycle invariants for tangles.
Definition 4.1
Let
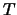
be a tangle and
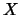
a quandle.
A (boundary-monochromatic)
coloring
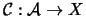
is a map from the set of arcs in a diagram of
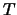
to
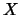
satisfying the same
quandle coloring condition as for knot diagrams at each crossing,
such that the (four) boundary points of the tangle diagram receives the same
element of
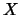
.
For a coloring 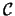 of a tangle diagram
of a tangle diagram 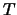 ,
a region colorings are defined in a similar manner as in the knot case.
In this case, we allow region colors to change (not necessarily
colored by the same element as the one assigned to the boundary points).
,
a region colorings are defined in a similar manner as in the knot case.
In this case, we allow region colors to change (not necessarily
colored by the same element as the one assigned to the boundary points).
Denote by
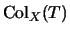 the set of colorings of a diagram of
the set of colorings of a diagram of 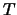 by
by 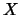 .
Denote by
.
Denote by
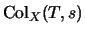 the set of colorings of a diagram of
the set of colorings of a diagram of 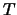 by
by 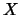 with the color of the leftmost region (between the boundary arcs NW and SW) being
with the color of the leftmost region (between the boundary arcs NW and SW) being 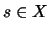 .
It is seen in a way similar to the knot case that the number of
colorings
.
It is seen in a way similar to the knot case that the number of
colorings
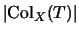 does not depend on a choice of a diagram of
does not depend on a choice of a diagram of 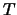 ,
and that the set of colorings are in one-to-one correspondence between
Reidemeister moves.
,
and that the set of colorings are in one-to-one correspondence between
Reidemeister moves.
The quandle 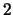 - and
- and 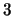 -cocycle invariants are defined for tangles in a
manner similar to the knot case, and denoted by
-cocycle invariants are defined for tangles in a
manner similar to the knot case, and denoted by
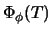 .
.
Definition 4.2
The inclusion of multisets are denoted by
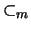
.
Specifically, if an element
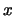
is repeated
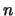
times in a multiset,
call
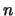
the multiplicity of
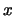
, then
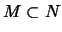
for multisets
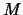
,
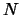
means that
if
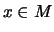
, then
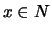
and the multiplicity of
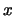
in
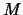
is less than or equal
to the multiplicity of
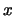
in
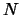
.
Theorem 4.3
Let
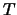
be a tangle and
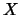
a quandle.
Suppose
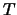
embeds in a link
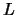
.
Then we have the inclusion
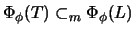
.
Proof.
Suppose a diagram of 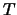 embeds in a diagram of
embeds in a diagram of 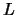 .
We continue to use
.
We continue to use 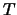 and
and 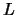 for these diagrams.
For a coloring
for these diagrams.
For a coloring 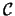 of
of 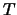 , let
, let 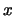 be the color of the boundary points.
Then there is a unique coloring
be the color of the boundary points.
Then there is a unique coloring 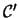 of
of 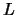 such that the restriction of
such that the restriction of 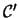 on
on 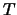 is
is 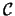 and all the arcs of
and all the arcs of 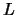 outside of
outside of 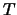 receive the color
receive the color 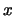 .
Then the contribution of
.
Then the contribution of
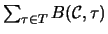 to
to
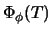 is equal to the contribution
is equal to the contribution
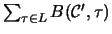 to
to
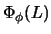 ,
and the theorem follows.
,
and the theorem follows. 
In this project we examine the cocycle invariants of tangles in the table
and those of knots in the table that do not satisfy the condition of the
above theorem, detecting the tangles that do not embed in knots in the tables.



Next: Bibliography
Up: Quandle Cocycle Invariants and
Previous: Realizing tangle embeddings
Masahico Saito - Quandle Website
2005-10-04
![]() of a tangle diagram
of a tangle diagram ![]() ,
a region colorings are defined in a similar manner as in the knot case.
In this case, we allow region colors to change (not necessarily
colored by the same element as the one assigned to the boundary points).
,
a region colorings are defined in a similar manner as in the knot case.
In this case, we allow region colors to change (not necessarily
colored by the same element as the one assigned to the boundary points).