A COMPLETELY DISTRIBUTED SOLUTION TO
TURING'S LEOPARDS' SPOTS PROBLEM
BASED ON ASYNCHRONOUS ACTIVITY
AND LOCAL ENTROPY
REDUCTION.
The leopards' spots problem was posed and solved by Alan Turing [1952]. The
problem is to design a distributed process for a large number of cells leading
to the emergence of a global pattern [spots] -- without resorting to global
operations or information. Turing's solution involved a diffusion-reaction mechanism
on a regularly arranged continuum of cells. The dynamics of diffusion-reaction
is described and proved in terms of differential equations [Turing 1952, Murray
1989]. It has been demonstrated [fig. 3] recently in vitro [DeKepper 1990, Castets
et al. 1990, Lengyel & Epstein 1991, Pool 1991].
A second solution, which I believe to be new, is demonstrated here, with the
simulation program. A formal mathematical proof that the program’s algorithm
succeeds with probability = 1 will be available fall of 2000. Related mathematics
and similar arguments may be found in [Stark 1995].
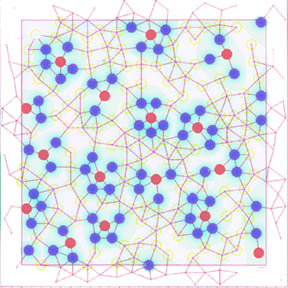
1. In this diagram vertices represent cells, edged
represent cell-cell communication [eg., gap junctions], and colors represent
cell states. This is a global pattern of cell-states in
a spot-like pattern. A spot is a single red cell totally surrounded by
a minimal set of blue cells. As a group, the red-blue configuration is surrounded
by a set of yellow cells which keeps the spots from touching and is minimal.
[There is a spot missing in this diagram and so the set of yellow cells is not
minimal. However, if the algorithm had run longer then the global pattern would
have contained the maximal number of spots and yellow would have been minimized.]
The only nontrivial part of this construction is to keep spots completely separated
by yellow – i.e., the blue cells surrounding one red cell must not be connected
to the blues surrounding another red cell. To avoid edge effects, the cells
are arranged on a torus – edges and vertices
in a margin are in the center square on the opposite side.
This solution is interesting for several reasons.
(1) It is based on the asynchronous activity of an arbitrarily large finite
set of cells.
(2) Cell and cell-to-cell communication is defined on a random graph (e.g.,
fig.1) of communicating cells by edge-transition rules.
(3) When active, a cell’s behavior [i.e., state transition] is determined by
its present state and the states of its neighbors.
(4) The cell program, if executed asynchronously, reduces
edge-state-pair entropy locally and ultimately globally. The algorithm fails if
cell activity is synchronous. Finally,
(5) the central role of entropy-reducing mechanisms in living systems, as proposed
by E. Schrödinger [1944] in his famous 1943 lecture series "What is Life"
at the Institute for Advanced Study in Dublin, is essential to this procedure.
The problem, as interpreted here, is to program cells so that in a random and
asynchronously active network they produce a global pattern. The cells cannot
have direct access to information beyond their state and the multi-set of neighboring
states. Spots are separated by yellow cells. In the initial state cell color
is random.
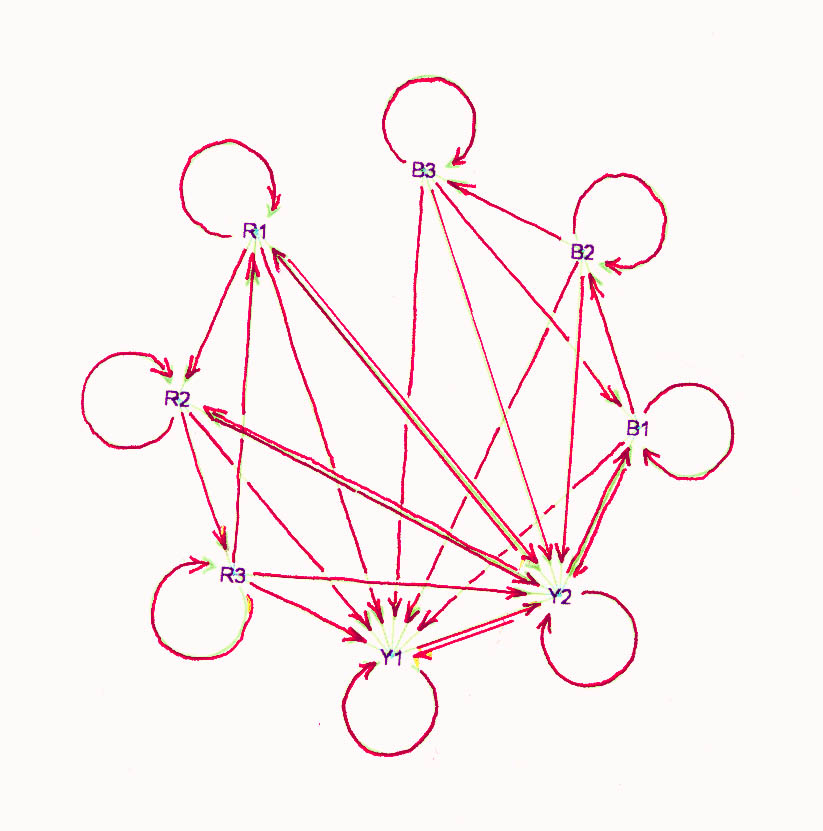
2. Red, blue, and yellow are the
phenotypes. Cell-states R1, R2, R3 appear red, B1, B2, B3 appear blue, and Y1,
Y2 appear yellow. So there are hidden variables. A red cell is stable if its
neighbors are all blue, a blue cell is stable if it has one red neighbor and at
least one yellow neighbor, and a yellow cell is stable if it has no red
neighbors. Stability involves the hidden variables too, but for now imagine that
active cells that are not stable move to Y1. This graph has no
automorphisms.
The algorithm’s program as a *.mws file [requires MAPLE 5 or later] and
instructions for use and experimentation are available from the author
[stark@math.usf.edu].
A cell-program which solves the problem is shown in the state-transition
diagram above with edge-rules described in section 2 of the attached program.
The spots to be computed consist have one red center cell completely surrounded
by a minimal set of blue cells. Spots are not allowed to touch.
The entropy mentioned above is the Shannon entropy of the measure space of
pairs {S[c],S[d]} of cell-states determined by cell-cell edges {c,d} and the
global state S. The solution presented here uses eight cell-states (two yellow
states Y1, Y2; three blue B1, B2, B3; and three red R1, R2, R3). This allows 36
unordered pairs. Edges (i.e., pairs of neighboring cells) in the random initial
state occur with probability 2/64 if the states are different and 1/64 if the
states are the same – e.g., P({Y1,Y1}) = 1/64 and P({Y1,B1}) = 2/64. The initial
entropy is about log(56) = 5.8 bits.
The final global states, as defined
above, have a probability measure which, P({Rj,Rk}), P({Yi,Rj}), and certain
other probabilities [a total of 21] are 0. The final entropy is then less than
log(35) = 5.1 bits – about 85% of the initial entropy. The reduction of global
entropy is much greater if a measure space of pairs {S[c], SoG[c]} of cell
states and multi-sets of neighboring states is used.
A cell is color-stable if (1) it is in one of the red states and all
of its neighbors are in a blue or Y2 state, or (2) if it is in a blue state Bi,
it has exactly one neighbor in a red state Rj (j=i+1 mod 3), it has no neighbor
in Bk (k=j+1 mod 3) nor in Y2, or (3) it is in Y1 and has no red and at least
one blue neighbor, or (4) it is in Y2 and has only yellow neighbors including at
least one Y1.
Active cells which are not color-stable tend to change to
Y1. [This produced a dramatic one-time reduction in the process’ entropy.] Cells
in Y1 surrounded by yellow cells change to Y2. Cells in Y2 which are surrounded
by Y2 neighbors only change to R1. Cells in Y2 with exactly one R1 neighbor and
no blue neighbors change to B1. Cells in Y2 with no red neighbors and at least
one blue neighbor change to Y1.
The algorithm published in [Stark 2000] does not separate spots. To correct
this, spots are dynamically cycling through their hidden variable. For example,
a spot’s cycle consists of
all B1 with R1 -> all B1 with R2 -> B1 or B2 with R2 -> all B2 with
R2 -> etc.
and two similar sequences of changes
all B1 with R1 ->…-> all B2 with R2 ->…-> all B3 with R3
->…-> all B1 with R1 ->
etc. But a spot will never have an B2 neighboring R1, or B3 neighboring R2,
or B1 neighboring R3. So if a cell in state B1 has neighbors in R2 and B3, then
it is because two spots are touching. In this case, the dissolution of one of
the spots begins with
the B1 cell changing to Y1. To guarantee this, the process must be
asynchronous. Ultimately, an attractor of global states is entered in which
the cells’ color is unchanging, all spots are properly formed, the no spots are
touching, and there is no space for another spot.

3. A computer-enhanced
image of an experimental Turing structure chemically-produced by Patrick De
Kepper, et al. University of Bordeaux, Physical Review Letters, summer 1990.
Simulation
For a text version of the simulation, click here.
To download a MAPLE version, right-click here.
References.
1944; Schrödinger, Erwin.; What is Life? , Cambridge University
Press, Cambridge, UK, [reprinted nearly 20 times since 1944].
1952; Turing, Alan; The chemical basis of morphogenesis, Phil. Trans.
Of the Royal Society, v. 237, pp. 5-72; London.
1989; Murray, James D., Mathematical Biology, Springer-Verlag, Berlin,
New York, etc.
1990; DeKepper, Patrick, et al., ???, Phys.Rev.Lett.,
v.??, p.??
1990; Castels, V; Experimental evidence of a sustained standing Turing-type
non-equilibrium chemical pattern, Phys.Rev.Lett., V. 64, p. 2953.
1990; Pool, R.; Did Turing discover how the leopard got its spots?, Science,
v. 251, p.627.
1991; Lengyel, Istvan & Irving Epstein; Modeling of Turing structures
in the chloride-iodide-malonic acid-starch reaction system, Science, v.
251, pp. 650-652.
1995; Stark, Richard;
Mathematics for a fundamental problem of biological information
processing, IEEE International Symposium on Intelligence in Neural and
Biological Systems, Herndon, VA.
2000; Stark, Richard & William Hughes; Asynchronous, irregular automata
nets: the path not taken; BioSystems; Elsevier, v.55, issues 1-3, pp. 107-117.
w richard stark, mathematics, university of south florida, tampa
33620, usa


