Analysis, Synthesis, and Doing Homework

In any kind of intellectual work -- in mathematics, political science, painting -- one takes things apart and puts things together. Consider the process of drawing a picture of an old man walking with a cane.

• You start with a sense of what the picture is going to be of. Many artists sketch a few preliminary (and very rough squiggle-like) drawings.
• Then you look at the parts of the picture: the cane, the arm on the cane (what is the angle of the wrist?) the expression on his face, the tilt of his hat, which leg his weight is on. Here we have sketches of pieces of the picture.
• Then there are the relations of the parts with each other. Is he leaning on the cane? How does the shadow cast by his hat cover his face? Now we get larger preliminary sketches, of his head's position on his neck (upright, forward?), of his free hand gesturing at chest height, etc.
• Then there are drafts of the drawing, until finally, the final drawing appears.

The word analysis comes from analyein, which is Greek for "to break up."

It is often helpful to break a problem or a phenomenon into small pieces: if one studied each piece, independently of the other pieces, one might have a better chance of understanding the pieces. From that, one might understand the whole.

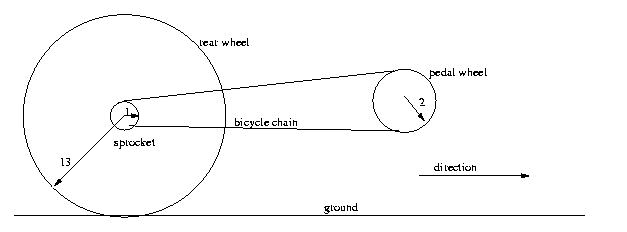
For example, suppose you were told that a bicyclist was pedalling so that the pedals went around once a second, and that the pedal wheel was two inches in radius, and that it was connected by the chain to the rear wheel via a sprocket wheel, and that the rear wheel was 13 inches diameter while the sprocket wheel was 1 inch in diameter. See the picture below:

Then suppose that you were asked how rapidly the bicycle was moving forward, in miles per hour.

Probably the easiest way to solve this problem is to break it into pieces, one piece for each wheel, perhaps as follows.

1. The pedal wheel is rotating once a second, so as its radius is 2 inches, its circumference is 4π inches, so it is pulling the chain at the rate of 4π inches per minute.
2. The chain is pulling the sprocket wheel at the rate of 4π inches per minute, so as the sprocket wheel has radius 1 inches and thus a circumference of 2π inches, it rotates 2 times a second.
3. The sprocket wheel is attached to the rear wheel, which thus also rotates 2 times a second. As the rear wheel is 13 inches in radius, its circumference is 26π inches, and so it pushes the ground past at 52π inches per second.
4. We convert to miles per hour. There are 12 times 5280 inches per mile, and 3600 seconds per hour, so the ground speed is 52π 3600/ 63360, which is about nine miles per hour.

We break problem into pieces I, II, III, ... We break piece I into sub-pieces A, B, C, ... We break sub-piece A into sub-sub-pieces 1, 2, 3, ... We break sub-sub-piece 1 into sub-sub-sub-pieces ... .....

The word synthesis comes from syntithenai, which is Greek for "to put together."

Knowledge is created, said John Locke in his Essay Concerning Human Understanding, by combining perceptions, ideas, and other bits of knowledge. Immanuel Kant, in his Critique of Pure Reason (see also his Prolegomena to any Future Metaphysics), imagined that there were two operations:

• Analysis. One understands something by taking it apart and looking at the pieces.
• Synthesis. One understands something by combining it or comparing it with other things, or by looking at interrelations between its constituent parts.

Eugene Wigner, in his The unreasonable effectiveness of Mathematics in the Natural Sciences, wrote that progress in physics would have been impossible if it wasn't possible to take phenomena apart and then study the parts in isolation. This is the essence of analysis.

There are two faces of synthesis. First, creative acts usually consist of combining notions that one usually doesn't imagine having much to do with each other. For example, if you have a model of the external combustion steam engine (pour water into hot piston chamber and it explodes into steam, pushing the piston up), and you want to construct an internal combustion engine (pour gasoline into piston chamber, ignite it and it explodes into carbon dioxide and steam, pushing the piston up), how do you get the gasoline into the chamber so it is distributed evenly? Not by pouring in measured amounts, surely. How about a perfume atomizer? Yes, Virginia, a carburetor is merely a very large atomizer. (This tale from James Burke, who is very fond of ... Connections.) This is one face of synthesis: the construction of entirely new things from old parts.

Second, many things cannot be understood in isolation, like the gears and spring of a mechanical clock. To understand a clock, one needs to took at the escapement wheel swinging forward impelled by the mainspring, a tooth caught in the escapement bar, itself swinging up and down, catching and releasing the wheel with the familiar tick tock tick tock.

Sometimes mathematics problems are like this, too. Consider the problem: find all solutions to:

3x + y = 2 -2y - z = 2 x = 1

This can be solved by substitution: x = 1, so y = 2 - 3 = -1, so z = 2 - 2 = 0, This is a reductionist approach: solve the problem variable. But what about:

x - y + 2z = 2 3x + 2y + z = 1 x + y + z = 0

Substitutions doesn't work so well here: we need to use a method that deals with the entire system at once: Cramer's rule, or the Gauss-Jordan method.

Contra Wigner (above), some things are not so readily taken apart. Sometimes, as many philosophers insist, the relations between things are important. The classic metaphor is the web or necklace of the Hindu thunder-god Indra: the web has many jewels, which reflect light to each other, so that we can see the entire web in each jewel. This makes some phenomena very difficult to analyze.

Actually, there is a third point that we should note. Carl Friedrich Hegel proposed a dialectic, which consists of taking the status quo view, the thesis, confronting it with and antithesis, and then resolving the two into a synthesis. Hegel's view was that we slowly work our way towards (never reaching) an Absolute. This suggests another view of synthesis: we have an object, and when we compare it to another object, we understand the first better.

• It is well known that a good way to understand one's own language better is to learn a foreign language. When one sees how different languages differ -- in English the adjective precedes the noun (the blue ribbon), while in French the adjective comes afterwards (la cordon bleu) -- one understands one's own language better.
• Also, your problem, and the other problem, are perhaps two examples of a "meta-problem." For example, to understand vertebrates, one looks at many different kinds of vertebrates. To understand Homo sapiens, one looks at cats, kangaroos, and canaries, and one sees how H. sapiens fits into the taxonomy of vertebrates.

The word thesis comes from tithenai, which is Greek for "to put or lay down."

Once all the work is done and you have lots of notes, sketches, studies, etc., you have to compile it in a coherent form so that people --- including yourself --- can understand it. Usually, this part of the job is dismissed as just the "writing up," as if the result somehow already exists in one's head, and all that one has to do is wave a magic wand over all the work and the result magically appears on paper. "The poem is in my head," says the frustrated poet. "I just can't get it on paper." The reality is that the poem is not in the poet's head, and it in fact isn't anywhere until it is on paper.

The thesis is the result of analysis and synthesis that you present to the world, and it does matter how it is presented. For example, a number of prescient scientific discoveries --- from Hermann Grassman's vector-like calculus to Gregor Mendel's laws of heredity --- were ignored by their contemporaries because of very bad presentation. Bertrand Russell may be right in saying that Benedict Spinoza was a deeper philosopher than John Locke, but it is not the profundity but the eye-glazing abstraction that costed Spinoza his audience until long after he died and was discovered by the public relations wunderkind Wolfgang Goethe.

Another aspect of thesis-construction is that the author himself may not understand what he is trying to say. Consider the sad case of Edward Blyth, who developed at least a preliminary version of the theory of natural selection. But he did not really figure out the dimensions of what he was dealing with, and it was Charles Darwin (and Alfred Wallace) who not only worked out the mechanism but also what its effects were, and then presented it in a way that other people could see its significance. (See Andy Bradbury's account of Darwin and Blyth.)

So the thesis is not just a putting down of the result of analysis and synthesis, it is also a matter of communication.

• You are communicating first of all with yourself. This aspect is not to be underestimated: even when writing up the result, their may be additional points to be explored, loose ends to be tied up, even (and this happens) errors to be exposed and corrected. You have to present to be clear to yourself.
• You are also presenting it to other people. It has to be organized so that other people can understand it. The usual procedure is to: tell them what you're going to tell them, tell them, and then tell them what you told them. So before going into a computation or a proof, outline what you're computing or proving; and afterwards, recapitulate.

So to recapitulate:

• First solve the problem, by taking it apart, by looking at how its pieces relate to eachother, how it is put together, and how it operates as a whole. Perhaps, also look at how it relates to other problems.
• Second, write up the solution in an accessible way.