samplewkstIVMaple8.html

Worksheet IV: Quandle Cocycle Knot Invariants

by Masahico Saito and Chad Smudde

This worksheet will explain the new procedures created for calculating quandle cocycle knot invariants of classical knots. Some of the procedure contained in this package are similar to those explained in the previous worksheet, but we have modified these to increase the speed at which the braids are colored. This was the main goal of this update. It is now possible to color braids with much larger quandles( ie. quandles with 25 elements or much more, over 100 elements, in some circumstances). The second major upgrade was creating easy to use procedures that would do mass calculations of these invariants at a minimal cost to the user. These procedures, once executed, could run for countless hours at no expense to the user and organize the data in a relatively efficient and effective manner. This worksheet should be considered a second version and compilation of the three previous worksheets. It is currently only configured to run in Linux. Porting to other O.S.'s is possible and may be simple in some cases. Explanations of why this is Linux specific and changes that should be made to allow use in other O.S.'s will be given throughout this worksheet

A web site was created to help organize this project. It can be found at http://shell.cas.usf.edu/quandle/. This web site contains a background section that briefly explains the theory that governs this topic. This worksheet is not intended to give such background information, but rather to explain how to use the procedures created to perform these calculations. One may also with to look at the book, ``Surfaces in 4-space,'' by Carter, Kamada, and Saito, Springer-Verlag, 2004. The reference section in the background section of the web page also contains many other references.

This worksheet is divided into the following sections:

I. Braids

II. Quandles

III. Coloring braids with C

IV. Calculating the value of the invariant
V. Mass calculations with automatic file name generation

First the package containing the procedures will be read into the worksheet. Note: If you place all of the files for this project in the same directory you will not need to specify the paths to them. The procedures contained in this package are listed here and explained in the appropriate section.

validColorVectors:=define_external(
                     'validcolorvectorsint',
                     'quandle'::ARRAY(datatype=integer[2]),
                     'quandlesize'::integer[4],
                     'knot'::ARRAY(datatype=integer[2]),
                     'braidindex'::integer[4],
                     'nopsknot'::integer[4],
                     'validCvecs'::ARRAY(datatype=integer[2]),
                     RETURN::integer[4],
                     LIB="ValCol8_1_05.so"):

cvrtarray:=proc(brind,nopknt,L,numVC);
Invar2_3UntwistedDLL:=proc(Quandle,p,Knot);
CalcUntwistinvars:=proc(filePATH,p ,qord,qnum,numberofknots,{cpath:=false},{solpath=false});
fpQuan:=proc(tfile,Quandle,qsize);
Invar2UntwistedDLL:=proc(Quandle,p,Knot);
Calc2Untwistinvars:=proc(filePATH,p,qord,qnum,numberofknots,{cpath=false},{solpath:=false});

Invar3UntwistedDLL:=proc(Quandle,p,Knot);

Calc3Untwistinvars:=proc(filePATH,p,qord,qnum,numberofknots,{cpath=false},{solpath:=false});
Invar2_3MochizukiDLL:=proc(Xpolym,Apolym,p,m1,m2,a3,n1,b2,Knot);
CalcMochinvars:=proc(filePATH,p ,polym,m1,m2,a3,n,b,numberofknots,{cpath:=false},{solpath:=false});
Invar2MochizukiDLL:=proc(Xpolym,Apolym,p,n1,b2,Knot);

Calc2Mochinvars:=proc(filePATH,p ,polym,n,b,numberofknots,{cpath:=false},{solpath:=false});

Invar3MochizukiDLL:=proc(Xpolym,Apolym,p,m1,m2,a3,Knot);

Calc3Mochinvars:=proc(filePATH,p ,polym,m1,m2,a3,numberofknots,{cpath:=false},{solpath:=false});
ismult:=proc(charstar);
CalcDihinvars:=proc(filePATH,p,numberofKnots,{cpath:=false},{solpath:=false});
co2TwistedSol:=proc(Quandle,polym,p);
Invar2TwistedDLL(Quandle,knot,polym,p);
Calc2twistinvars(filePATH,p,polym,qord,qnum,numberofknots,{cpath:=false},{solpath:=false});
tinverse(polym,p);

quandlesize:=proc(Quandle);
makeinv:=proc(Quandle);
co2Solution:=proc(Quandle,m::posint);
mirrorKnot:=proc(L);
barKnot:=proc(L);
connSumKnots:=proc(Knots_list);
co3Solution:=proc(Quandle,m::posint);
Mochizuki3coc:=proc(Xpolym,Apolym,p,m1,m2,a3);
cocycle3check:=proc(cocy,Xpolym,Apolym,p);
Xi:=proc(n);
Mochizuki2coc:=proc(Xpolym,Apolym,p,m1,a2);
cocycle2check:=proc(cocy,Xpolym,Apolym,p);
MochizukiDihedral3coc:=proc(p);

> restart;

> #Change the path to where you stored the package
read "/media/sda1/quancocDLLpkgmaple8.m":

This define external statement was not properly saved to the package. You will need to copy and paste it into any worksheet that you load the quancocDLLpkgmaple8.m package into. This is vital since most of the procedures depend on this define_external statement.

> #Change the path to where you saved the ValCol8_1_05.so file.

validColorVectors:=define_external(
                     'validcolorvectorsint',
                     'quandle'::ARRAY(datatype=integer[2]),
                     'quandlesize'::integer[4],
                     'knot'::ARRAY(datatype=integer[2]),
                     'braidindex'::integer[4],
                     'nopsknot'::integer[4],
                     'validCvecs'::ARRAY(datatype=integer[2]),
                     RETURN::integer[4],
                     LIB="/media/sda1/WorksheetIV/ValCol8_1_05.so"):

This procedure was not included into the package. It is used in section 3 of this worksheet. It is mostly for demonstration purposes.

> printColors:=proc(Knot,Col,numVc)
local i,j,k,brind,q,r,ss,threeprint;

brind:=max(op(map(x->abs(x),Knot)))+1;
q:=iquo(numVc,3);
r:=numVc mod 3;
i:=1;
for ss from 1 to q do
i:=ss*3-2;
    for j from 1 to nops(Knot) +1 do
        for threeprint from 1 to 3 do
         for k from 1 to brind do
            printf("%5d",Col[i][j][k] );
         od;
        i:=i+1;
        printf("\t\t");
od;
i:=i-3;
printf("\n");
od;

printf("\n\n");
od;
i:=ss*3-2;
#for ss from 1 to r do
    for j from 1 to nops(Knot) +1 do
        for threeprint from 1 to r do
         for k from 1 to brind do
            printf("%5d",Col[i][j][k] );
         od;
        i:=i+1;
        printf("\t\t");
od;
i:=i-r;
printf("\n");
od;
printf("\n\n");
#od;

end:

I. Braids

Worksheet III was where we saw the change in braids. We changed to the table of braids generated form Charles Livingstons's Knotinfo database. This allowed us to increase the number of knots we use to those with 12 and fewer crossings. We also added the knot name and the Alexander polynomial to the data stored for each knot. Printing the knot name with the value of the invariant allows us to more easily recognize the knot that was calculated. Adding the Alexander polynomial to the data file was motivated by Inoue's theorem. Procedures for braid manipulation are also included in this package.

        The procedures and files pertaining to braids are:
              knotsLivingston.txt
              mirrorKnot(),
              barKnot(),
              connSumKnots().

First read the knot data into the worksheet.
Note: A colon should be used here to avoid printing the 2977 different knots.

> #Alter path here

read "/media/sda1/WorksheetIV/knotsLivingston.txt":

The data is stored in a two dimensional array that has the name "Knot". The data is accessed by the command, [> Knot[i,j]; . The first index, i, specifies the knot you wish to access. i ranges from 0 to 2976. The knots were ordered as they appeared in Charles Livingston's Knotinfo database. The second index, j, ranges from 1 to 3. j=1 will give the knot name which is stored as a string. j=2 will give the braid word. This is stored as a list indexed by one. j=3 will give the Alexander polynomial of the knot. This was not stored as a string, but as an expression so that it will be of type polynom when read into Maple.

The trefoil knot.

> Knot[0,1];

> Knot[0,2];

> Knot[0,3];

The final knot available.

> Knot[2976,1];Knot[2976,2];Knot[2976,3];

> type(Knot[0,3],polynom);

Since the Alexander polynomial is of type polynom, we can check the gcd with some other polynomial that may be used for the Alexander quandle. See Inoue's theorem for more information.

> Gcd(Knot[0,3],t^2-t+1) mod 2;

The mirror image is obtained with the procedure mirrorKnot(). This procedure will only work on the braid word of the knot. Any naming must be performed manually. The procedure will return the braid word for the mirror image of the given braid.

> mirrorKnot(Knot[1,2]);

The braid with orientation reversed can be obtained with the procedure, barKnot(). This will also only work on the braid word of the knot. Any naming should be performed manually.

> barKnot(Knot[1,2]);

The procedure connSumKnots takes a list of lists as is argument. The elements of the list are the braid words that are to be connected in the specified order.

Note: This procedure just connects the braids. It does NOT try to reduce the length. The new braid word is returned as a single list indexed by one..

> connSumKnots([Knot[0,2],Knot[1,2]]);

Note: special procedures for calculating the braid index or number of crossings of a given braid are not included since this information can be obtained from simple calls.

The braid index is recovered from the call.

> brind:=max(op(map(x->abs(x),Knot[0,2])))+1;

The number of crossings.

> nops(Knot[0,2]);

II. Quandles

There are two different files that will give us access to quandles. The first is "Quandle." This is the same file that was used in worksheets I and II (the untwisted and twisted cases). The second is the package used to generate the Cayley table for certain Alexander Quandles. This is the one used in worksheet III, the Mochizuki polynomial cocycle case.

Read the quandles into the worksheet from the file "Quandle."

The file "Quandle" contains all quandles from three to six elements that are pairwise non-isomorphic with non-trivial torsion part in its second or third homology groups. The list is from the book ``Surfaces in 4-space,'' by Carter, Kamada, Saito, Springer-Verlag, 2004. They are labeled Qi_j where i is the size and j is which quandle. There are 25 six element, 6 five element, 3 four element, and 1 three element quandles in the file "Quandle.m". These are two dimensional zero indexed arrays representing the multiplication table a*b for a,b in X, the quandle. This step could be skipped if you don't want to work with any quandle in this list.

Note: A colon should be used to avoid printing all of the data.

> #alter path here

read "/media/sda1/WorksheetIV/Quandle":

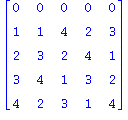
> print(convert(Q3,matrix));

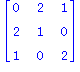
> print(convert(Q5_4,matrix));

Read the Alexander quandle package into the worksheet.

> #alter path here

read "/media/sda1/WorksheetIV/alexQuanpkg.m";

Recall that Z_p[t,t^-1]/(h(t)) where h(t)=a_0+a_1*t+...+a_n*t^n is a polynomial in t with quandle operation a*b=ta+(1-t)b is a finite quandle. The procedure AlexQuandle() will generate the Cayley table for this quandle and return an isomorphic quandle whose Cayley table has elements in {0..n-1} where n is the order of the quandle. This will allow us to reuse old programs that are set to only accept quandles that are zero indexed two dimensional arrays with elements in {0..n-1}.

Since p is prime and h(t)=a_0+a_1*t+...+a_n*t^n is a polynomial (in t), elements of Z_p[t,t^-1]/(h(t)) are represented by the reduced residue system, i.e., polynomials of the form b_0+b_1*t+...+b_(n-1)*t^(n-1) where b_i is in Z_p. Since p is prime 1..p-1 are units in Z_p, so that we can solve (t^(-1))*h(t)=0 for t^-1. This implies that t^(-1) is expressed by a polynomial as above, and every element is represented by a polynomial of a positive degree. Then by taking the remainder when divided by h(t), every element is represented by a polynomial as above. The purpose of the local procedure rres() is to list all such polynomials. Next, the procedure Alexmult() will multiply all possibilities a*b where a, b are in the reduced residue system. The resulting polynomial will then be reduced back into the reduced residue system. Finally, the procedure findelt() will find that polynomial in the list of reduced residues and return that integer value.

> Q9:=AlexQuandle(t^2-t+1,3);

> convert(Q9,matrix);

This procedure can also be used to generate the Dihedral quandles since the Dihedral quandle is the special case when h(t)=t+1.

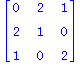
> R3:=AlexQuandle(t+1,3);

> print(convert(R3,matrix));

The following command may be useful for calculating the order of the quandle. This will avoid the user from specifying the order in the case that the quandle is passed to a procedure. This command is unnecessary for the procedures included here, but may be useful for procedure you create.

> quandleorder:=linalg[coldim](convert(R3,matrix));

> linalg[coldim](convert(Q9,matrix));

III. Coloring braids with C

This is the most exciting upgrade to this project. Since the complexity of coloring braids with quandles is O(c|X|^n) where |X| is the order of the quandle and n is the braid index, the time required to quickly calculate the values of the invariant become limited very fast. For example, |X|=8 presents problems and when |X|=25 knots with a braid index of 3 are almost impossible to calculate. This package will use a c program that was compiled as a shared object file, ValCol8_1_05.so (dynamic link library in other O.S.'s), and then linked to Maple with the define_external procedure, validColorVectors(). This greatly increased the size of the quandles we can work with.

This program will only color the braids of the knot. Some issues regarding the coloring of the regions will be discussed below.

The rest of this section explains how this is accomplished. Knowledge of this material does not limit ones ability to use the other procedures. This is all hidden in the functioning of the procedures that calculate the values of the invariants. This will however be necessary if one wishes to create his or her own procedures that use this C coloring program.

The C source code for the braid coloring program is printed below with a system call.
Note: This is Linux specific since the cat function is used.

This program will generate all possible initial color vectors and then color a given braid. Only the valid color vectors are saved. These color vectors are then stored in an array (pointer) validCvecs that is passed to the c program from this Maple procedure. The parameters used in the define_external are now explained. The fist element ''validcolorvectorsint' is the name of the function that was used in the c program. 'quandle' is the Cayley table for the quandle that is used. Arrays must be modified slightly before passing them to the c program. Assume you have a quandle, Quandle:=Q3 := array(0 .. 2, 0 .. 2,[(2, 1)=0,(0, 0)=0,(2, 2)=2,(0, 1)=2,(0, 2)=1,(1, 0)=2,(1, 1)=1,(1, 2)=0,(2, 0)=1]); stored as in the previous worksheets. Now the quandle should be modified to QuandleC by the following statement, QuandleC:=Array(op(Quandle),datatype=integer[2],order=C_order): This will change the datatype to a 2 byte integer and store it in C_order (one dimensional zero indexed array). This will allow the c program to use it. All arrays passed to this function must be modified in this way. The second term 'quandlesize' is an integer representing the order of the quandle. 'knot' is an array that is the braid word for the knot. It must be modified as the quandle array was before passing it. Next the braid index and the number of crossings, 'braidindex' and 'nopsknot' respectively, are integers. Finally, an empty array validCvecs' is created and passed to the function. This is really just a pointer that will be used to store that valid color vectors. This array can be initialized by the following statement, VALIDCOLORS:=Array(0..10000000,datatype=integer[2],order=C_order):
This array is declared with a bound to it (10000000 in this example). Statically declaring the array makes things easier, but may create problems under special cases. For example, it requires (braidindex * nops(Knot)+1) many cells of the array to store the valid color vectors for one valid coloring of the braid. So if the # valid colorings is greater than 10000000/(braidindex*nops(Knot)+1) then a segmentation fault will be created with the c program and then passed to the Maple program. This is not a good programming practice, but it will work for now given our other constraints. There are some possible modifications that can be made without rewriting the c program. One such solution would be to allocate more memory for the validCvecs array. The above example allotted 10000000 cells at 2 bytes each. This requires 20 MB of space. So if your computer has enough memory you could simply declare a larger array. There are other solutions to this problem. If this turns out to be a frequently encountered problem, we will rework this. I have ideas already, but I feel this is a good alpha version. The function will return an integer representing the number of valid colorings for the braid. This is a 4 byte integer and should not exceed 2^31 -1. The shared object file "ValCol8_1_05.so" should be stored in the same directory as the worksheet calling it to avoid altering the PATH given to the LIB statement below.

> #alter path here to location of the c file.

DD:=ssystem("cat /media/sda1/WorksheetIV/libcolor8_1_05.c"):DD[2];

After the C program was created and compiled as a "shared object" file a Maple procedure calling this program needed to be created. The procedure validColorVectors:=define_external() is this procedure. The following example will find all valid color vectors of the trefoil knot when colored with the three element Dihedral quandle, R3.

First convert the Quandle to the appropriate datatype.

> QuandleC:=Array(op(R3),datatype=integer[2],order=C_order);

$QuandleC := Array(0 .. 2, 0 .. 2, {(2, 2) = 2, (0, 1) = 2, (0, 2) = 1, (1, 0) = 2, (1, 1) = 1, (2, 0) = 1}, datatype = integer[2], storage = rectangular, order = C_order)$
$QuandleC := Array(0 .. 2, 0 .. 2, {(2, 2) = 2, (0, 1) = 2, (0, 2) = 1, (1, 0) = 2, (1, 1) = 1, (2, 0) = 1}, datatype = integer[2], storage = rectangular, order = C_order)$

Next convert the knot to the appropriate datatype.

> KnotC:=Array(0..(nops(Knot[0,2])-1),Knot[0,2],datatype=integer[2],order=C_order);

$KnotC := Array(0 .. 2, {(0) = 1, (1) = 1, (2) = 1}, datatype = integer[2], storage = rectangular, order = C_order)$
$KnotC := Array(0 .. 2, {(0) = 1, (1) = 1, (2) = 1}, datatype = integer[2], storage = rectangular, order = C_order)$

Now we need a place to store the valid color vectors that the C program will find (a pointer). Notice how the Memory tab in the bottom right of the window will jump after this declaration.

> VALIDCOLORS:=Array(0..10000000,datatype=integer[2],order=C_order);

Now for the magic! We call the program to calculate the valid color vectors.

> Knot[0,2];
quandleorder:=linalg[coldim](convert(R3,matrix));
brind:=max(op(map(x->abs(x),Knot[0,2])))+1;
numcross:=nops(Knot[0,2]);

> numVcolors:=validColorVectors(QuandleC,quandleorder,KnotC,brind,numcross,VALIDCOLORS):

The number of valid colorings is the return type. In this example we assigned this to the variable numVcolors.

> numVcolors;

So the trefoil has 9 valid colorings when colored with the 3 element Dihedral quandle. Recall that the number of colorings of a knot with a quandle is an invariant in itself. This procedure could be used by itself to calculate the values of that invariant.

The array that is holding the valid color vectors was passed to the procedure. We allocated to much space for this (intentionally). The value stored in the array will not print since the array is so large.

> VALIDCOLORS;

There were only 9 valid colorings in this case, so there should be data in 72 cells of the array. Any cells beyond this point are zero. The value that they were initialized to.

> for i from 0 to 10*4*2 do
printf("%d",VALIDCOLORS[i]);
od;

000000000100221102001122001122001111111112110022102211002122001122222222200000000

So we have the valid colorings, but they are stored in an undesirable way and we using a lot of memory that is not necessary. We will not use the procedure cvrtarray() to manipulate the data and store it in a better way. The procedure cvrtarray:=proc(brind,nopknt,L,numVC) must be passed the braid index, number of crossing, the VALIDCOLORS obtained from the validColorVectors() call, and finally the number of valid colorings (the value returned from the procedure validColorVectors()). We will assign the valid coloring to the array called Colors.

> Colors:=cvrtarray(2,3,VALIDCOLORS,numVcolors);

The array Colors is a three dimensional array, Colors[i][j][k]. The first index, i, ranges from 1 to the number of valid colorings. The second and third are the position of the braid where that color was assigned. The procedure printColors:=proc(Knot,Col,numVc) will print these colorings.

> printColors(Knot[0,2],Colors,numVcolors);

0 0 1 0 2 0

0 0 0 2 0 1

0 0 2 1 1 2

0 0 1 0 2 0

0 1 1 1 2 1

1 2 1 1 1 0

2 0 1 1 0 2

0 1 1 1 2 1

0 2 1 2 2 2

2 1 2 0 2 2

1 0 0 1 2 2

0 2 1 2 2 2

Now lets examine the time it takes to color when we use much larger quandles.

This first example will color the figure eight knot with a 25 element quandle, Z_5[t,t^(-1)]/(t^2-t+1). We will use two system calls to the "date" function to examine the time required for the c program to check which of the 15625 possible initial color vectors produce valid colorings. This system call is Linux specific.

> Q25:=AlexQuandle(t^2-t+1,5):
QuandleC:=Array(op(Q25),datatype=integer[2],order=C_order):
KnotC:=Array(0..(nops(Knot[1,2])-1),Knot[1,2],datatype=integer[2],order=C_order):
VALIDCOLORS:=Array(0..10000000,datatype=integer[2],order=C_order):
Knot[1,1];Knot[1,2];
quandleorder:=linalg[coldim](convert(Q25,matrix)):
brind:=max(op(map(x->abs(x),Knot[1,2])))+1:
numcross:=nops(Knot[1,2]):
HH:=ssystem(date):HH[2];
numVcolors:=validColorVectors(QuandleC,quandleorder,KnotC,brind,numcross,VALIDCOLORS):
HH:=ssystem(date):HH[2];
numVcolors;

This only had the trivial colorings. We can see them with the following commands.

> Colors:=cvrtarray(3,4,VALIDCOLORS,numVcolors):
printColors(Knot[1,2],Colors,numVcolors);

0 0 0 1 1 1 2 2 2

3 3 3 4 4 4 5 5 5

6 6 6 7 7 7 8 8 8

9 9 9 10 10 10 11 11 11

12 12 12 13 13 13 14 14 14

15 15 15 16 16 16 17 17 17

18 18 18 19 19 19 20 20 20

21 21 21 22 22 22 23 23 23

24 24 24

It took less than one second to check all of the possible colorings, and it found that only 25 ( the trivial ones) were valid.

That was too fast!! Since the complexity is O(c|X|^braidindex), lets increase the size of the quandle to 256 elements and use the same knot (braid index of 3).
This example should not take to long.

> Q256:=AlexQuandle(t^8+1,2):
QuandleC:=Array(op(Q256),datatype=integer[2],order=C_order):
KnotC:=Array(0..(nops(Knot[1,2])-1),Knot[1,2],datatype=integer[2],order=C_order):
VALIDCOLORS:=Array(0..10000000,datatype=integer[2],order=C_order):
Knot[1,1];Knot[1,2];
quandleorder:=linalg[coldim](convert(Q256,matrix)):
brind:=max(op(map(x->abs(x),Knot[1,2])))+1:
numcross:=nops(Knot[1,2]):
HH:=ssystem(date):HH[2];
numVcolors:=validColorVectors(QuandleC,quandleorder,KnotC,brind,numcross,VALIDCOLORS):
HH:=ssystem(date):HH[2];
numVcolors;

The time stamps shows that it takes about 12 seconds (on my computer also this time will vary) to calculate the valid colorings. FAST!! FAST!! When you run this it did take longer than that however. This is mostly due to the cost of generating the Cayley table for the quandle. Increasing the braid index will obviously slow this program down much faster than increasing the size of the quandle. This example only had to generate and check 16777216 many colorings. Using the 25 element quandle above with knot "10_35" would require generating and checking 244140625 possible colorings. This took about 13 minutes (on my computer). You can uncomment out the below execution group if you wish to run this example.

> #Q25:=AlexQuandle(t^2-t+1,5):
#QuandleC:=Array(op(Q25),datatype=integer[2],order=C_order):
#KnotC:=Array(0..(nops(Knot[118,2])-1),Knot[118,2],datatype=integer[2],order=C_order):
#VALIDCOLORS:=Array(0..10000000,datatype=integer[2],order=C_order):
#Knot[118,1];Knot[118,2];
#quandleorder:=linalg[coldim](convert(Q25,matrix)):
#brind:=max(op(map(x->abs(x),Knot[118,2])))+1:
#numcross:=nops(Knot[118,2]):
#HH:=ssystem(date):HH[2];
#numVcolors:=validColorVectors(QuandleC,quandleorder,KnotC,brind,numcross,VALIDCOLORS):
#HH:=ssystem(date):HH[2];
#numVcolors;

IV. Calculating the value of the invariant

This section covers the procedures:

Invar2_3UntwistedDLL:=proc(Quandle,p,Knot);
Invar2UntwistedDLL:=proc(Quandle,p,Knot);
Invar3UntwistedDLL:=proc(Quandle,p,Knot);

Invar2_3MochizukiDLL:=proc(Xpolym,Apolym,p,m1,m2,a3,n1,b2,Knot);
Invar2MochizukiDLL:=proc(Xpolym,Apolym,p,n1,b2,Knot);

Invar3MochizukiDLL:=proc(Xpolym,Apolym,p,m1,m2,a3,Knot);
Invar2TwistedDLL(Quandle,knot,polym,p);.
Each of these procedures will calculate the value of the invariant for a specific knot for the given cocycle case. The coloring is performed with the c program and hidden from the user. These programs are otherwise similar to that in the previous worksheets. When it made sense, procedures calculating the 2-cocycle and 3-cocycle cases at the same time were created. The colorings of the regions is done with Maple. This was intentional since we know that there are |X|*m, where |X| is the order of the quandle and m is the number of valid colorings of the braid, validcolorings when shadow coloring. Since the number of valid colorings of the braid is usually small, relatively speaking, the cost for coloring the regions should be small. Hence the decision to use Maple. There are examples where this approach has created trouble, high time cost. Coloring of the regions with c will help and will be implemented soon.

Untwisted case

The procedure Invar2_3UntwistedDLL:=proc(Quandle,p,Knot) will solve the 2-cocycle and 3-cocycle conditions and calculate the values of each of the invariants. The procedure requires three parameters. The first is the quandle passed as before, a two dimensional zero indexed array representing the Cayley table of the quandle. The second is the prime modulus for the Coefficient group, Z_p. Finally the knot in braid form. This procedure will return 6 items. The first and second are the values of the untwisted 2-cocycle invariant and untwisted 3-cocycle invariant, respectively. The third is the valid coloring of the braid. Fourth and fifth are the solutions to the 2 and 3-cocycle conditions. Finally, the number of valid coloring of the braid is returned. By assigning these values to a list we can access only the desired data.

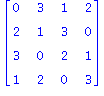
This example will calculate value of the untwisted 2 and 3-cocycle invariant for the figure eight knot with the quandle Q4_3 and coefficient group Z_2.

> print(convert(Q4_3,Matrix));
Knot[1,1];Knot[1,2];
Items:=Invar2_3UntwistedDLL(Q4_3,2,Knot[1,2]);

First we get the value of the untwisted 2-cocycle invariant from Items[1].

> Items[1];

We get the value of the untwisted 3-cocycle invariant from Items[2].

> Items[2];

Note: The t[i] in the values of the invariant are free variables obtained from solving the cocycle conditions. They take values from the Z_p. By assigning values to these free variables we are in essence choosing a specific cocycle and getting a specific value. This output is a family of values of invariants.

If one chooses the valid coloring of the braid can then be saved or viewed. We will use the print Colors() procedure to view the 16 different colorings of the braid here. The number of valid coloring of the braid is Items[6].

> printColors(Knot[1,2],Items[3],Items[6]);

0 0 0 3 1 0 1 2 0

0 0 0 1 2 0 2 3 0

0 0 0 1 3 2 2 1 3

0 0 0 3 0 2 1 0 3

0 0 0 3 1 0 1 2 0

2 3 0 2 0 1 1 1 1

3 1 0 0 3 1 1 1 1

3 2 1 0 2 3 1 1 1

2 0 1 2 1 3 1 1 1

2 3 0 2 0 1 1 1 1

3 2 1 0 3 1 3 0 2

2 0 1 3 2 1 0 1 2

2 3 0 3 0 2 0 3 1

3 1 0 0 1 2 3 2 1

3 2 1 0 3 1 3 0 2

0 1 2 2 2 2 1 3 2

1 3 2 2 2 2 3 0 2

1 0 3 2 2 2 3 1 0

0 2 3 2 2 2 1 2 0

0 1 2 2 2 2 1 3 2

1 0 3 2 1 3 0 2 3

0 2 3 1 0 3 2 1 3

0 1 2 1 2 0 2 0 1

1 3 2 2 3 0 0 3 1

1 0 3 2 1 3 0 2 3

3 3 3

The solutions to the untwisted 2-cocycle condition is Items[4].

> print(Items[4]);

The solutions to the untwisted 3-cocycle conditions is Items[5].

> print(Items[5]);

The procedures Invar2UntwistedDLL:=proc(Quandle,p,Knot) and Invar3UntwistedDLL:=proc(Quandle,p,Knot) require the same arguments to be passed, but they only calculate the 2 or 3-cocycle case, respectively. They return 4 items: the value of the invariant, the valid coloring of the braid, the solutions to the untwisted condition, and the number of valid coloring of the braid.

We will now look at the untwisted 3-cocycle invariant for the trefoil with quandle Q5_4 and coefficient group Z_2.

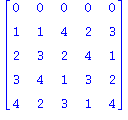
> print(convert(Q5_4,matrix));
Knot[0,1];
Knot[0,2];
L:=Invar3UntwistedDLL(Q5_4,2,Knot[0,2]);

The value of the untwisted 3-cocycle invariant.

> L[1];

Recall that this procedure only returns the colorings of the braids, L[2], and the number of valid colorings of the braid, L[4]. Not the colors and number of colorings of the braid and regions. The 2-cocycle case is similar.

Twisted Case

There is only one procedure for this case, the twisted 2-cocycle. The form that the value of the invariant is returned in has changed some from the version that appeared in worksheet II. In worksheet II the value was returned as a multiset where the elements were the state-sum contribution of a specific coloring. The value that is returned now will appear more like the untwisted case. This procedure requires the following: Quandle, Knot, polynomial in t for the coefficient group, and prime modulus for the coefficient group. The return type is similar to the untwisted 2-cocycle case.

Let's look at an example. We will use the quandle Q3 for the knot "6_1" and coefficient group Z_3[t,t^(-1)]/(t^2+1).

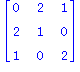
> print(convert(Q3,matrix));
Knot[4,1];
Knot[4,2];
K:=Invar2TwistedDLL(Q3,Knot[4,2],t^2+1,3);

The value of the twisted 2-cocycle invariant for the quandle Q3 for the knot "6_1" and coefficient group Z_3[t,t^(-1)]/(t^2+1).

> K[1];

The x[i] are free variable introduced when solving the twisted 2-cocycle conditions. These free variable are carried over to the value of the invariant. t is the indeterminate from the coefficient group. By assigning values to these free variables we get a specific element of the coefficient group.

The nine valid colorings of the braid.

> printColors(Knot[4,2],K[2],K[4]);

0 0 0 0 0 1 1 0 0 2 2 0

0 0 0 0 1 2 1 0 2 1 2 0

0 0 0 0 2 0 1 0 1 0 2 0

0 0 0 0 2 1 2 0 1 2 1 0

0 0 0 0 0 2 2 0 0 1 1 0

0 0 0 0 0 2 1 2 0 1 2 1

0 0 0 0 0 1 0 2 0 2 0 1

0 0 0 0 0 1 1 0 0 2 2 0

1 0 0 1 1 1 1 1 1 2 2 1

0 2 0 1 1 1 1 1 2 0 2 1

2 1 0 1 1 1 1 1 0 1 2 1

2 0 2 1 1 1 1 1 0 2 0 1

1 2 2 1 1 1 1 1 1 0 0 1

1 2 0 2 1 1 1 1 1 0 2 0

1 0 1 2 1 1 1 1 1 2 1 0

1 0 0 1 1 1 1 1 1 2 2 1

2 0 0 2 2 1 1 2 2 2 2 2

0 1 0 2 1 0 1 2 2 2 2 2

1 2 0 2 0 2 1 2 2 2 2 2

1 0 1 2 0 1 0 2 2 2 2 2

2 1 1 2 2 0 0 2 2 2 2 2

2 1 0 1 2 0 1 0 2 2 2 2

2 0 2 1 2 1 2 0 2 2 2 2

2 0 0 2 2 1 1 2 2 2 2 2

The solutions to the twisted 2-cocycle conditions.

> print(K[3]);

Mochizuki polynomial cocycle case

In this case, both the 2 and 3-cocycles make sense. So we have three procedures to calculate these values, Invar2_3MochizukiDLL:=proc(Xpolym,Apolym,p,m1,m2,a3,n1,b2,Knot), Invar2MochizukiDLL:=proc(Xpolym,Apolym,p,n1,b2,Knot), and Invar3MochizukiDLL:=proc(Xpolym,Apolym,p,m1,m2,a3,Knot). The procedure, Invar2_3MochizukiDLL(), for calculating the 2-cocycle and 3-cocycle case at the same time will be described. The other procedures are similar for the individual cases. Xpolym is a polynomial in t used for the Alexander quandle used for coloring the braids. Apolym is the polynomial in t used for the coefficient group. p is the prime modulus used for both the Alexander quandle and coefficient group. m1, m2, and a3 correspond to the exponents from Mochizuki's 3-cocycle formula, f(x,y,z)=(x-y)^(p^m1) * (y-z)^(p^m2) * z^(a3). This procedure will check that the Mochizuki condition are satisfied. ie. Apolym divides 1-t^((p^m1)+(p^m2)+a_3) mod p where a3 is a power of p or that a3=0. n1 and b2 correspond to the exponents for the Mochizuki 2-cocycle formula,

f(x,y)=(x-y)^(p^n1) * y^(b2). The Mochizuki 2-cocycle conditions are also checked in this case. The six items returned are ordered like the untwisted case.

This example will calculate the values of the invariants for the trefoil knot where the quandle and coefficient group are Z_2[t,t^(-1)]/(t^2-t+1) The 2-cocycle formula is f(x,y)=(x-y)^2 * y so we assign the values n1=1, b2=1. The3-cocycle formula is f(x,y,z)=(x-y)^ * (y-z)^2 so we assign the values m1=0, m2=1, a3=0.

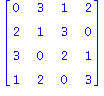
> print(convert(AlexQuandle(t^2-t+1,2),matrix));
Knot[0,1];
Knot[0,2];
L:=Invar2_3MochizukiDLL(t^2-t+1,t^2-t+1,2,0,1,0,1,1,Knot[0,2]);

The value of the 2-cocycle invariant with quandle and coefficient group Z_2[t,t^(-1)]/(t^2-t+1) for the trefoil knot and 2-cocycle formula f(x,y)=(x-y)^2 * y is the first item returned.

> L[1];

The value of the 3-cocycle invariant with quandle and coefficient group Z_2[t,t^(-1)]/(t^2-t+1) for the trefoil knot and 3-cocycle formula

f(x,y,z)=(x-y)^ * (y-z)^2 is the second item returned.

> L[2];

The exponents of u in the value of the invariant are elements of the coefficient group Z_2[t,t^(-1)]/(t^2-t+1). t is the indeterminate. It is not a free variable. You will not encounter any free variables in this case. So in the 2-cocycle case there were 4 coloring that contributed the zero in Z_2[t,t^(-1)]/(t^2-t+1) as their state-sum contribution and 12 coloring that contributed t+1 in Z_2[t,t^(-1)]/(t^2-t+1) as their state-sum contribution.

Once again the colors are just the valid coloring of the braid. We will print these by using the third element returned and the sixth, number of valid colorings.

> printColors(Knot[0,2],L[3],L[6]);

0 0 1 0 2 0

0 0 0 2 0 3

0 0 2 1 3 2

0 0 1 0 2 0

3 0 0 1 1 1

0 1 1 3 1 1

1 3 3 0 1 1

3 0 0 1 1 1

2 1 3 1 0 2

1 0 1 2 2 1

0 2 2 3 1 0

2 1 3 1 0 2

1 2 2 2 3 2

2 3 2 2 2 0

3 1 2 2 0 3

1 2 2 2 3 2

0 3 1 3 2 3

3 2 3 0 3 1

2 0 0 1 1 2

0 3 1 3 2 3

3 3

The fourth and fifth items returned are the values from the Mochizuki formula's.

Mochizuki polynomial cocycle for Dihedral quandles

There is not a special procedure for this case since it can be calculated by nesting other procedures. We will use the untwisted 3-cocycle procedure, Invar3UntwistedDLL:=proc(Quandle,p,Knot), for this case. This procedure had an optional fourth argument that was the cocycles. So if we use the procedure, MochizukiDihedral3coc:=proc(p), to calculate the values from the Mochizuki formula, f[i,j,k]:=((i-j)*((2*k^p-j^p)-(2*k-j)^p)/p) mod p and pass these as the fourth parameter we can calculate this case.

This example is with the quandle R7, seven element Dihedral quandle, and the knot 5_2.

> Knot[3,1];
Knot[3,2];
M:=Invar3UntwistedDLL(AlexQuandle(t+1,7),7,Knot[3,2],MochizukiDihedral3coc(7));

The value of the 3-cocycle invariant

> M[1];

V. Mass calculations with automatic file name generation

This worksheet and procedures were originally written with Maple 10. The keyword optional parameters were not supported with Maple 8. in the list of procedures below, you can spot these by,{cpath=false},{solpath:=false}. I modified the code for the procedures so that this worksheet will function with Maple 8. Now the cpath and solpath are required parameters. they do not have an initial value. More about this later in this section.
This section consider the following procedures:
CalcUntwistinvars:=proc(filePATH,p ,qord,qnum,numberofknots,{cpath=false},{solpath:=false});
Calc2Untwistinvars:=proc(filePATH,p,qord,qnum,numberofknots,{cpath=false},{solpath:=false});

Calc3Untwistinvars:=proc(filePATH,p,qord,qnum,numberofknots,{cpath=false},{solpath:=false});
CalcMochinvars:=proc(filePATH,p ,polym,m1,m2,a3,n,b,numberofknots,{cpath:=false},{solpath:=false});

Calc2Mochinvars:=proc(filePATH,p ,polym,n,b,numberofknots,{cpath:=false},{solpath:=false});

Calc3Mochinvars:=proc(filePATH,p ,polym,m1,m2,a3,numberofknots,{cpath:=false},{solpath:=false});
CalcDihinvars:=proc(filePATH,p,numberofKnots,{cpath:=false},{solpath:=false});
Calc2twistinvars(filePATH,p,polym,qord,qnum,numberofknots,{cpath:=false},{solpath:=false});.

These procedures will calculate the values of the invariants, generate a file, and write the values to that file. There are options for writing the valid colorings and/ or the solutions of the cocycle to a file also. The first parameter is common to all of these procedures. filePATH is the path to the directory where you wish to save the files for the invariants. This is of type string. numberofknots is also a common parameter. All of these procedures start by calculating the value of the trefoil knot. These procedures will then calculate the values for all knots up to numberofknots. For example, numberofknots=83 will calculate the values for all knots with 9 and fewer crossings (248 for knots with 10 a fewer crossings, 800 for 11 and fewer, and 2976 for 12 and fewer). Any other place you whish to stop in that range can also be chosen. The other common parameter cpath and solpath will be explained below.

The untwisted case has three procedures CalcUntwistinvars:=proc(filePATH,p ,qord,qnum,numberofknots,{cpath:=false},{solpath=false}), Calc2Untwistinvars:=proc(filePATH,p,qord,qnum,numberofknots,{cpath=false},{solpath:=false}), and Calc3Untwistinvars:=proc(filePATH,p,qord,qnum,numberofknots,{cpath=false},{solpath:=false}). These are for calculating both 2 and 3 cocycle case, 2 cocycle case only, and 3 cocycle case only, respectively. All of these require the same parameters. The prime modulus for the coefficient group is, p. Recall that the quandle in the file "Quandle" were stored with names Qi_j where i was the size of the quandle and j was the order that it appeared in the list. the parameter qord corresponds to i and qnum corresponds to j. Note: this restricts these three procedures to only work with the quandles Q4_1 to Q6_25 from the file "Quandle". By altering these procedure you can obtain other possibilities.

I wish to organize all of the files containing invariants in the directory /home/csmudde/Invariants/ on my machine. I have also created two subdirectories here to store color and solution files (to be described later). I will assign this path to the variable MyDirectory as a string so I can avoid rewriting it throughout these examples. This directory must exist on your machine. These procedures will NOT create a directory for you.

> #change this to a valid directory on your machine!!!
MyDirectory:="/home/csmudde/Invariants/";

For demonstration purposes, I will use system calls to show you the contents of the directories and files. You may wish to skip these system calls and just use your favorite text editor and file manager to se the results. I will comment these out, so if you wish to execute the system calls you will need to alter the paths and uncomment these statements
ls is a Linux command to list files and subdirectories in the specified directory. You will see the two subdirectories that I created and no files.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants"):tempHolder[2];

Now I will calculate the untwisted 2 and 3 cocycle invariants for the quandle Q5_4 with coefficient group Z_2 for the first 10 knots in the list.

> CalcUntwistinvars(MyDirectory,2 ,5,4,10,false,false);

/home/csmudde/Invariants/Z_2untwistedQ5_4_2cocinv.inv

/home/csmudde/Invariants/Z_2untwistedQ5_4_3cocinv.inv

There should now be two files in the directory you specified. They will have the names that were printed above. Everyone of these procedures will print the file name that it creates and writes the data containing the values of the invariants. These files are given a .inv extension. This will make it easier to manage your files. These files are just text files and have a hidden extension as txt.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants"):tempHolder[2];

The files for the untwisted cases are named with the coefficient group first the word untwisted, the quandle Qqord_qnum, then an underscore with the case 2cocinv or 3cocinv. The two procedures Calc2Untwistinvars() and Calc3Untwistinvars() are similar, but they only calculate one case.

Next we will use the cat function to print the contents of the file for the 3-cocycle case that was created in the previous example. A header is created for any file that these programs create. This header should contain enough information to allow the user to determine the contents of the file. The knot name , braid word used, and finally the value of the invariant are listed.

> tmpcat:=ssystem("cat /home/csmudde/Invariants/Z_2untwistedQ5_4_3cocinv.inv"):tmpcat[2];

The Mochizuki polynomial cases also contain three procedures, CalcMochinvars:=proc(filePATH,p ,polym,m1,m2,a3,n,b,numberofknots,{cpath:=false},{solpath:=false}), Calc2Mochinvars:=proc(filePATH,p ,polym,n,b,numberofknots,{cpath:=false},{solpath:=false}), and Calc3Mochinvars:=proc(filePATH,p ,polym,m1,m2,a3,numberofknots,{cpath:=false},{solpath:=false}). The parameters are the same as described in section IV of this worksheet.

This example will calculate the values of the invariants for the first 10 knots where the quandle and coefficient group are Z_2[t,t^(-1)]/(t^2-t+1) The 2-cocycle formula is f(x,y)=(x-y)^2 * y so we assign the values n1=1, b2=1. The3-cocycle formula is f(x,y,z)=(x-y)^ * (y-z)^2 so we assign the values m1=0, m2=1, a3=0.

> CalcMochinvars(MyDirectory,2,t^2-t+1,0,1,0,1,1,10,false,false);

/home/csmudde/Invariants/Z_2mod(t^2-t+1)2cocinv1_1.inv

/home/csmudde/Invariants/Z_2mod(t^2-t+1)3cocinv0_1_0.inv

These procedures will calculate the values for the invariant only if the Gcd(g(t), Delta(K)) mod p <> 1 where g(t) is the polynomial used for the quandle and Delta(K) is the Alexander polynomial for the knot K (stored in Knot[i,3]). This is motivated by Inoue's theorem. You should now see the two above named files in your directory. These files are name by the quandle, then the case 2 cocycle or 3 cocycle by 2coc or 3 coc, and finally by the exponents that you choose for the Mochizuki formulas.

A header is created for any invariant file that these procedures creates. It should contain all the information to allow you to distinguish the case that was calculated. The knot number, the braid word used, and the value of the invariant appear for each knot calculated.

The 5 element Dihedral quandle for the first 10 knots with the Mochizuki cocycle formula for Dihedral quandles.

> CalcDihinvars(MyDirectory,5,10,false,false);

/home/csmudde/Invariants/MochDih_R_53coc_inZ_5.inv

A system call to see the contents of our directory.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants"):tempHolder[2];

The twisted example for the first 10 knots with coefficient group Z_2[t,t^(-1)]/(t^3+t+1) with quandle Q4_1. In this example you use qord and qnum to specific the quandle from the file "Quandle."

> Calc2twistinvars(MyDirectory,2,t^3+t+1,4,1,10,false,false);

/home/csmudde/Invariants/Z_2modt^3+t+1twistedQ4_1_2cocinv.inv

Now we should have 5 different files containing values for invariants for different cases.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants"):tempHolder[2];

The second to last parameter in these procedures is for the color files. The last parameter is for the solution files. These parameter do NOT have a default value, so if you do not wish to use these features, you need to pass, false, to the procedure in its position in the argument list. These parameters allow the user to specify a path to a directory where the color data or solution data can be written. If you wish to use these features you can pass the path to the procedure as follows: "/home/csmudde/Invariants/colorings/" for the path to the color files or "/home/csmudde/Invariants/solutions/" for the path to the solution files. The files containing the valid colorings is given the extension .clr and the solutions files are given a .sol extension. Both of these are really just text files. The data is written in a way that will allow the user to read the data into a Maple worksheet as Maple input. One can then use that data for further calculations avoiding the overhead of recalculating the data (ie. recalculating the valid color vectors).

This example will write the solutions to the cocycle condition to a file. I will create a variable to store the path where I wish to write the solution files.

> MySolutions:="/home/csmudde/Invariants/solutions/";

Note this directory is currently empty.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants/solutions/"):tempHolder[2];

I will now set solpath=MySolutions. solpath is a optional keyword parameter that was initialized to false. Note: we do NOT use the assignment operator ":=". Now solpath will not evaluate to false and the solutions file will be created and written to the directory you specify.

> Calc2Mochinvars(MyDirectory,3,t^2+1,1,1,10,false,MySolutions);

/home/csmudde/Invariants/solutions/coc2SolnsZ_3mod(t^2+1)_1_1.sol

/home/csmudde/Invariants/Z_3mod(t^2+1)2cocinv1_1.inv

Lets see the contents of the solutions directory.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants/solutions/"):tempHolder[2];

Now lets see the contents of this solution file.

> #uncomment and alter filePATH
tempHolder:=ssystem("cat /home/csmudde/Invariants/solutions/coc2SolnsZ_3mod(t^2+1)_1_1.sol"):tempHolder[2];

Notice how the header file and time stamps are commented out. This will allow use to read this data into a Maple session. All of these procedures have the ability to write the solutions to a file. This option is most useful in the twisted and untwisted cases since the cost associated in solving the cocycle conditions is high. The Mochizuki polynomial cases can be calculated vary fast; however, testing the solutions requires some time.

We now look at an example where we write the valid colorings of the braids to a file.

> MyColorfiles:="/home/csmudde/Invariants/colorings/";

This directory is currently empty.

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants/colorings"):tempHolder[2];

In this example we will use the 3 element Dihedral quandle with the Mochizuki formula for cocycles for the first ten knots. This formula is for 3 cocycles, but the colorings for the regions are not written to the file. Only the colorings of the braids are written.

> CalcDihinvars(MyDirectory,3,10,MyColorfiles,false);

/home/csmudde/Invariants/MochDih_R_33coc_inZ_3.inv

> #uncomment and alter filePATH
tempHolder:=ssystem("ls /home/csmudde/Invariants/colorings"):tempHolder[2];

The colorings for a given braid are written to its own file. Since a small quandle was used, these files are small (less than 10 KB). When larger quandles are used and the braid has many valid colorings with that quandle, the size of the color file can increase (50MB or more). These files are also created so that they could be read into a Maple worksheet for use with different cocycles thus eliminating the cost of finding valid colorings.

> #uncomment and alter filePATH
tempHolder:=ssystem("cat /home/csmudde/Invariants/colorings/ColorDih_R_3K4_1.clr"):tempHolder[2];

This example only had the trivial colorings. Files containing nontrivial colorings can become very long. Once again, using this cat function is for demonstration proposes only. Use you text editor to view the contents of these files. It will save you time!!

Final Notes. These programs do not allow one to pass the valid coloring to them. This will be a feature in a future update. This will be a nice feature because it will allow use to examine how different cocycles effect the value of the invariant for a given braid and quandle. We will not have the exponential cost of evaluating the colorings since you will pass them to the procedure. We will also have to write the C program to calculate the colorings of the regions. The C program for calculating the valid colorings of the braids allowed use to calculate with larger quandles than expected. So the assumption that Maple could color the regions fast was false. This will also be a great update! Programs for calculating other Alexander quandles may also be included. This package is currently limited to work only with primes p. The updates made here allow use to calculate many, many more values so this is a good stopping point for this update.