


Next: Addition and closure of
Up: Preliminary
Previous: Preliminary
Again we refer the reader to
the article posted at http://shell.cas.usf.edu/quandle
under the title Background, for the following terms we use:
quandles, Alexander quandles, colorings of knot diagrams, coloring of
regions of a knot diagram, quandle 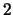 - and
- and 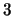 -cocycles,
-cocycles,
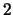 - and
- and 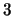 -cocycle invariants of knots.
-cocycle invariants of knots.
Here we review a definition of cocycle invariants in terms of multisets,
that will be used in this article.
Let 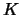 be a knot diagram on the plane.
Let
be a knot diagram on the plane.
Let 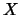 be a finite quandle and
be a finite quandle and 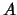 an abelian group.
Let
an abelian group.
Let
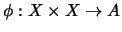 be a quandle
be a quandle 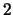 -cocycle, which can be regarded as
a function satisfying the
-cocycle, which can be regarded as
a function satisfying the 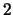 -cocycle condition
-cocycle condition
and
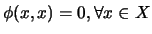 .
Let
.
Let 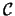 be a coloring of a given knot diagram
be a coloring of a given knot diagram 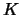 by
by 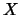 .
The Boltzmann weight
.
The Boltzmann weight
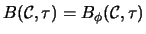 at a crossing
at a crossing 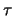 of
of 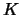 is then defined by
is then defined by
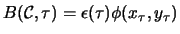 ,
where
,
where 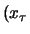 ,
, 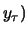 is the ordered pair of colors at
is the ordered pair of colors at 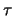 and
and
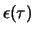 is the sign (
is the sign (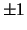 ) of
) of 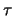 .
Then the
.
Then the 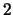 -cocycle invariant
-cocycle invariant
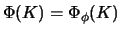 in a multiset form is defined by
where
in a multiset form is defined by
where
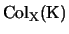 denotes the set of colorings of
denotes the set of colorings of 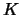 by
by 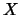 .
(A multiset a collection of elements where a single element can be repeated
multiple times, such as
.
(A multiset a collection of elements where a single element can be repeated
multiple times, such as
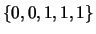 ).
).
Let
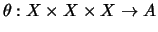 be a quandle
be a quandle 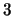 -cocycle, which can be regarded as
a function satisfying
-cocycle, which can be regarded as
a function satisfying
and
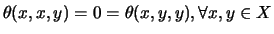 .
.
Let 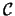 be a coloring of arcs and regions of a given diagram
be a coloring of arcs and regions of a given diagram 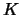 .
Let
.
Let
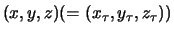 be the ordered triple of colors
at a crossing
be the ordered triple of colors
at a crossing 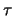 .
Then the weight in this case is defined by
.
Then the weight in this case is defined by
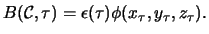 The (
The (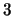 -)cocycle invariant is defined in a similar way to
-)cocycle invariant is defined in a similar way to 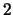 -cocycle invariants by
the multiset
-cocycle invariants by
the multiset
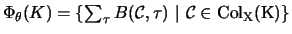 ,
where
,
where
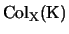 denotes the set of colorings with region colors
of
denotes the set of colorings with region colors
of 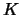 by
by 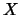 .
.



Next: Addition and closure of
Up: Preliminary
Previous: Preliminary
Masahico Saito - Quandle Website
2005-10-04
![]() be a knot diagram on the plane.
Let
be a knot diagram on the plane.
Let ![]() be a finite quandle and
be a finite quandle and ![]() an abelian group.
Let
an abelian group.
Let
![]() be a quandle
be a quandle ![]() -cocycle, which can be regarded as
a function satisfying the
-cocycle, which can be regarded as
a function satisfying the ![]() -cocycle condition
-cocycle condition
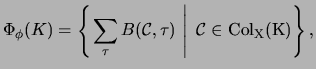
![]() be a quandle
be a quandle ![]() -cocycle, which can be regarded as
a function satisfying
-cocycle, which can be regarded as
a function satisfying
![]() be a coloring of arcs and regions of a given diagram
be a coloring of arcs and regions of a given diagram ![]() .
Let
.
Let
![]() be the ordered triple of colors
at a crossing
be the ordered triple of colors
at a crossing ![]() .
Then the weight in this case is defined by
.
Then the weight in this case is defined by
![]() The (
The (![]() -)cocycle invariant is defined in a similar way to
-)cocycle invariant is defined in a similar way to ![]() -cocycle invariants by
the multiset
-cocycle invariants by
the multiset
![]() ,
where
,
where
![]() denotes the set of colorings with region colors
of
denotes the set of colorings with region colors
of ![]() by
by ![]() .
.